Zadanie nr 4828473
O zdarzeniach losowych 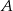 i
i 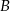 wiadomo, że
wiadomo, że 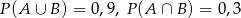 i
i 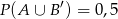 . Oblicz
. Oblicz 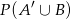 .
.
Rozwiązanie
Sposób I
Zaznaczmy na diagramie Venna zbiory 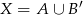 i
i 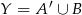 .
.
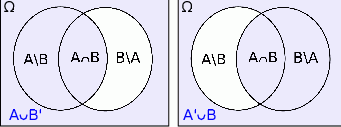
Z obrazka widać, że

Zatem
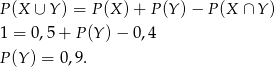
Sposób II
Jak poprzednio zaznaczamy zbiory 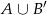 i
i 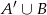 na diagramie Venna. Z diagramu widzimy, że
na diagramie Venna. Z diagramu widzimy, że
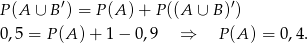
Podobnie
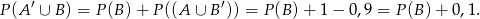
Musimy zatem obliczyć 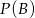 – nie ma z tym jednak problemu, bo znamy
– nie ma z tym jednak problemu, bo znamy 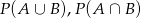 i
i 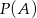 . Zatem
. Zatem
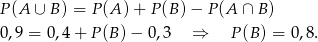
Stąd
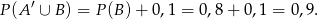
Sposób III
Ponownie rozpoczynamy od naszkicowania diagramu Venna.
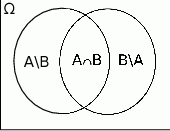
Na mocy wzoru na prawdopodobieństwo sumy zdarzeń mamy
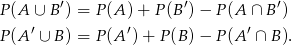
Rzut oka na diagram Venna i możemy te równości przepisać w postaci
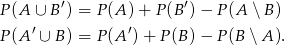
Dodajmy teraz te równości stronami
![P(A ∪ B ′)+ P (A ′ ∪ B) = = P(A ) + P(A ′)+ P(B ′) + P(B )− [P (A ∖ B) + P (B ∖A )] = = 1+ 1− [P (A ∪ B )− P (A ∩ B )].](https://img.zadania.info/zad/4828473/HzadR17x.gif)
Zatem
![0,5+ P(A ′ ∪ B ) = 2− [0,9 − 0 ,3 ] ⇒ P (A ′ ∪ B) = 0,9.](https://img.zadania.info/zad/4828473/HzadR18x.gif)
Odpowiedź: