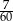Zadanie nr 4888077
Zakupiono 16 biletów do teatru, w tym 10 biletów na miejsca od 1. do 10. w pierwszym rzędzie i 6 biletów na miejsca od 11. do 16. w szesnastym rzędzie. Jakie jest prawdopodobieństwo zdarzenia polegającego na tym, że 2 wylosowane bilety, spośród szesnastu, będą biletami na sąsiadujące miejsca?
Rozwiązanie
Sposób I
Przyjmijmy za zdarzenia elementarne nieuporządkowane pary wylosowanych biletów. Mamy wtedy
Jest dokładnie 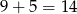 zdarzeń sprzyjających (9 par w pierwszym rzędzie i 5 w szesnastym), więc interesujące nas prawdopodobieństwo jest równe
zdarzeń sprzyjających (9 par w pierwszym rzędzie i 5 w szesnastym), więc interesujące nas prawdopodobieństwo jest równe
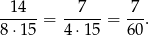
Sposób II
Tym razem za zdarzenia elementarne przyjmijmy pary uporządkowane wylosowanych biletów. Mamy zatem
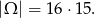
Wśród zakupionych biletów jest 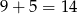 par biletów na sąsiadujące miejsca (9 par w pierwszym rzędzie i 5 w szesnastym), co daje nam
par biletów na sąsiadujące miejsca (9 par w pierwszym rzędzie i 5 w szesnastym), co daje nam 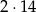 par uporządkowanych (bilety możemy w takiej parze umieścić na 2 sposoby). Interesujące nas prawdopodobieństwo jest równe
par uporządkowanych (bilety możemy w takiej parze umieścić na 2 sposoby). Interesujące nas prawdopodobieństwo jest równe
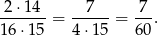
Odpowiedź: