Zadanie nr 5094498
Rzucamy  razy monetą symetryczną. Jakie jest prawdopodobieństwo, że orzeł wypadnie nieparzystą liczbę razy?
razy monetą symetryczną. Jakie jest prawdopodobieństwo, że orzeł wypadnie nieparzystą liczbę razy?
Rozwiązanie
Liczba orłów może być parzysta lub nieparzysta, czyli prawdopodobieństwo wynosi 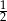 . Brzmi naiwnie? – z pewnością tak, ale jak się okaże jest w tym dużo prawdy.
. Brzmi naiwnie? – z pewnością tak, ale jak się okaże jest w tym dużo prawdy.
Sposób I
Jeżeli myślimy o wynikach doświadczenia jak o ciągach długości  , to mamy
, to mamy
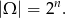
Ile jest zdarzeń sprzyjających? – na pierwszych 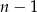 monetach może być cokolwiek, a na
monetach może być cokolwiek, a na  –tej monecie nie mamy już wyboru (w zależności od ilości orłów na poprzednich musi być na niej orzeł lub reszka). Zatem prawdopodobieństwo wynosi.
–tej monecie nie mamy już wyboru (w zależności od ilości orłów na poprzednich musi być na niej orzeł lub reszka). Zatem prawdopodobieństwo wynosi.
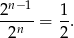
Sposób II
Możemy sobie myśleć, że mamy schemat Bernoullego. Powiedzmy, że sukcesem nazywamy wyrzucenie orła. Pytamy jakie jest prawdpodobieństwo otrzymania nieparzystej liczby sukcesów. Liczymy
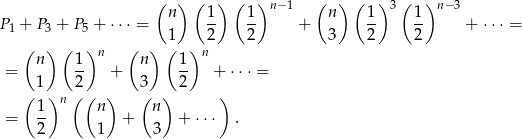
Aby obliczyć sumę w nawiasie korzystamy z dwumianu Newtona
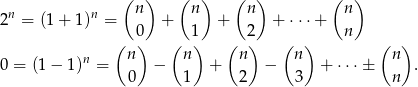
Pierwsza równość mówi, że suma wszystkich symboli Newtona 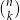 z ustalonym
z ustalonym  jest równa
jest równa 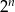 , a druga, że suma tych z parzystym
, a druga, że suma tych z parzystym 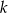 jest taka sama jak suma tych z nieparzystym
jest taka sama jak suma tych z nieparzystym 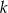 . Zatem intersująca nas suma jest równa
. Zatem intersująca nas suma jest równa
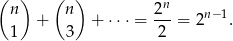
Prawdopodobieństwo wynosi
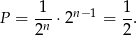
Sposób III
Jeżeli wiemy jaki jest wynik, to możemy prawdopodobieństwo wyliczyć indukcyjnie. Dla 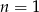 sprawa jest jasna. Powiedzmy teraz, że rzucamy
sprawa jest jasna. Powiedzmy teraz, że rzucamy 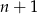 monetami i wiemy, że nieparzysta liczba orłów na
monetami i wiemy, że nieparzysta liczba orłów na  pierwszych monetach pojawia się z prawdopodobieństwem
pierwszych monetach pojawia się z prawdopodobieństwem 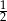 . Zatem z tym samym prawdopodobieństwem pojawia się parzysta liczba orłów. Zakładając którąkolwiek z tych sytuacji, mamy 50% szans na to, że będzie nieparzysta liczba orłów (na
. Zatem z tym samym prawdopodobieństwem pojawia się parzysta liczba orłów. Zakładając którąkolwiek z tych sytuacji, mamy 50% szans na to, że będzie nieparzysta liczba orłów (na 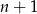 monecie musi być reszka lub orzeł odpowiednio). Zatem ze wzoru na prawdopodobieństwo całkowite mamy
monecie musi być reszka lub orzeł odpowiednio). Zatem ze wzoru na prawdopodobieństwo całkowite mamy
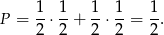
Odpowiedź: