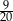/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 5126594

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są dwa pudełka: czerwone i niebieskie. W każdym z tych pudełek znajduje się 10 kul ponumerowanych liczbami od 1 do 10. Z każdego pudełka losujemy jedną kulę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że numer kuli wylosowanej z czerwonego pudełka jest mniejszy od numeru kuli wylosowanej z niebieskiego pudełka.

Rozwiązanie

Wszystkich zdarzeń elementarnych jest

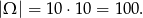
|Ω | = 10⋅1 0 = 100.

Policzmy ile jest zdarzeń sprzyjających.

Sposób I

Jeżeli z niebieskiego pudełka wyciągniemy 10, to z czerwonego możemy wyjąć dowolną liczbę mniejszą od 10; jeżeli z niebieskiego wyciągniemy 9, to z czerwonego możemy wyjąć dowolną liczbę mniejszą od 9 itd. Zdarzeń sprzyjających jest więc

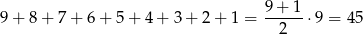
9 + 1 9 + 8 + 7 + 6 + 5 + 4+ 3+ 2+ 1 = ------⋅9 = 4 5 2

(skorzystaliśmy ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego). Prawdopodobieństwo jest więc równe

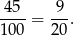
45 9 ----= ---. 100 20

Sposób II

W wyniku opisanego losowania możemy otrzymać jedną z trzech sytuacji:

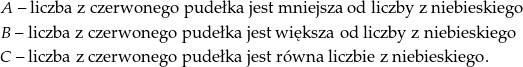
A – liczba z czerwonego pude łka jest mniejsza od liczby z niebieskiego B – liczba z czerwonego pude łka jest większa od liczby z niebieskiego C – liczba z czerwonego pude łka jest równa liczbie z niebieskiego.

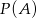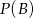Ponieważ w obu pudełkach jest tyle samo liczb, prawdopodobieństwa P (A ) i P (B) są równe, ponadto

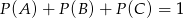
P (A )+ P (B) + P (C) = 1

(bo nie ma innych możliwości). Zatem

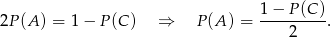
1−--P(C-) 2P (A ) = 1 − P(C ) ⇒ P (A) = 2 .

Prawdopodobieństwo zdarzenia 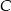C jest za to bardzo łatwo obliczyć – jest dokładnie 10 zdarzeń sprzyjających: (1,1),(2,2) itd. Zatem

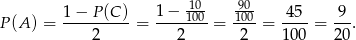
1 − P (C) 1 − 11000 91000- 45 9 P(A ) = --------- = ------- = ---= ----= ---. 2 2 2 100 20

Sposób III

Zauważmy, że jeżeli mamy dwie różne liczby ze zbioru 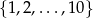{ 1,2,...,10} to możemy dokładnie na jeden sposób zrobić z nich wynik zdarzenia sprzyjającego: mniejsza z nich musi być liczbą wylosowaną z czerwonego pudełka, a większa musi być wyciągnięta z niebieskiego pudełka. To oznacza, że jest

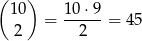
( 10) 10 ⋅9 = ------= 45 2 2

zdarzeń sprzyjających i prawdopodobieństwo jest równe

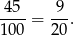
45 9 ----= ---. 100 20

 
Odpowiedź: -9 20

Wersja PDF