/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 5489579

Dodaj do ulubionych
Dodaj do rozwiązanych

Umieszczamy króla szachowego w lewym dolnym rogu 64-polowej szachownicy, a następnie siedem razy przesuwamy go losowo w górę lub w prawo (za każdym razem na nowo losujemy kierunek przesunięcia).

PIC

Zakładając, że wylosowanie każdego kierunku jest jednakowo prawdopodobne, oblicz prawdopodobieństwo, że na końcu król nie znajdzie się w rogu szachownicy.

Rozwiązanie

Łatwiej będzie nam policzyć prawdopodobieństwo 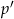′ p zdarzenia przeciwnego A ′ .

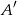Zdarzenia sprzyjające 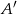A ′ to takie, że król jest w jednym z dwóch rogów rogów szachownicy (lewym górnym lub prawym dolnym). Ponieważ do każdego rogu może dojść dokładnie w jeden sposób, więc są dwa zdarzenia sprzyjające ′ A .

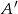Policzmy teraz ile jest wszystkich zdarzeń elementarnych. Zauważmy, że w każdym momencie mamy dokładnie dwie możliwości wyboru dalszej drogi, czyli wszystkich możliwych dróg jest 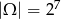|Ω | = 27 i prawdopodobieństwo wynosi

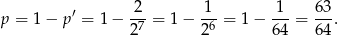
′ 2 1 1 63 p = 1 − p = 1 − -7-= 1 − -6-= 1− ---= --. 2 2 64 64

 
Odpowiedź: 63 64

Wersja PDF