/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 5574657

Dodaj do ulubionych
Dodaj do rozwiązanych

Z pewnej grupy osób, w której jest dwa razy więcej mężczyzn niż kobiet, wybrano losowo dwuosobową delegację. Prawdopodobieństwo tego, że w delegacji znajdą się tylko kobiety jest równe 0,1. Oblicz, ile kobiet i ilu mężczyzn jest w tej grupie.

Rozwiązanie

Oznaczmy liczbę kobiet przez 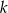k . Zatem mężczyzn jest 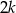2k . Jeżeli za zdarzenia elementarne przyjmiemy niepuorządkowane pary wylosowanych osób, to

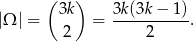
( ) 3k 3k(3k-−-1-) |Ω | = 2 = 2 .

Prrawdopodobieństwo wylosowania dwóch kobiet wynosi

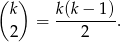
( ) k k(k−-1-)- 2 = 2 .

Zatem

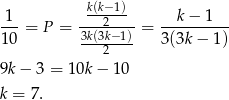
k(k−-1) -1- = P = ---2----= --k-−-1--- 1 0 3k(3k−-1) 3(3k − 1 ) 2 9k − 3 = 10k− 10 k = 7 .

 
Odpowiedź: Jest 7 kobiet i 14 mężczyzn

Wersja PDF