Zadanie nr 5631953

Z talii 52 kart losujemy bez zwracania dwie karty. Jakie jest prawdopodobieństwo wylosowania dwóch asów?

Rozwiązanie

Sposób I

Przyjmijmy za zdarzenia elementarne dwuelementowe zbiory wylosowanych kart. Mamy zatem

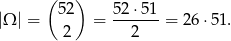
( ) 52 52⋅ 51 |Ω | = = -------= 26 ⋅51. 2 2

W sumie są cztery asy, dwa z nich można wybrać na

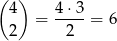
(4 ) 4⋅ 3 = ---- = 6 2 2

sposobów. Zatem prawdopodobieństwo wynosi

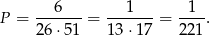
6 1 1 P = ------- = -------= ----. 2 6⋅5 1 13 ⋅17 221

Sposób II

Tym razem za zdarzenia elementarne przyjmijmy uporządkowane pary wylosowanych kart. Ponieważ losujemy bez zwracania mamy

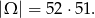
|Ω | = 52 ⋅51.

Pierwszego asa możemy wybrać na 4 sposoby, a drugiego na 3. Zatem

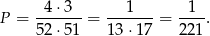
--4⋅3-- ---1--- -1-- P = 5 2⋅5 1 = 13 ⋅17 = 221 .

Sposób III

Liczymy interesujące nas prawdopodobieństwo ze wzoru na prawdopodobieństwo warunkowe.

Najpierw losujemy jedną kartę całej talii. Prawdopodobieństwo otrzymania asa jest równe

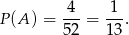
4 1 P (A) = ---= --. 52 13

Teraz losujemy drugą kartę z pozostałych kart – niech 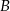oznacza zdarzenie polegające na wyciągnięciu asa w tym drugi losowaniu. Mamy zatem

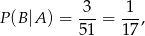
3 1 P (B |A ) = ---= --, 51 17

a interesujące nas prawdopodobieństwo jest równe

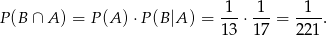
1 1 1 P(B ∩ A ) = P (A) ⋅P(B |A) = 13-⋅17-= 221-.

Odpowiedź: -1- 221