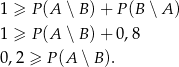/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 5686973

Dodaj do ulubionych
Dodaj do rozwiązanych

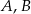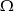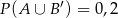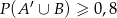Zdarzenia losowe A ,B są zawarte w Ω oraz ′ P (A ∪ B ) = 0 ,2 . Wykaż, że P (A ′ ∪ B) ≥ 0,8 .

Rozwiązanie

Rysujemy diagram Venna

PIC

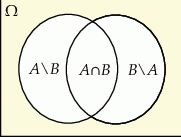
Sposób I

Zauważmy, że 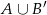A ∪ B′ jest zdarzeniem nie mniejszym niż 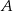A , zatem

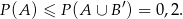
P (A ) ≤ P(A ∪ B′) = 0,2.

Stąd

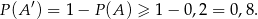
P (A′) = 1 − P (A) ≥ 1− 0,2 = 0,8.

Teraz wystarczy zauważyć, że

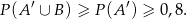
P (A ′ ∪ B ) ≥ P (A′) ≥ 0,8.

Sposób II

Tym razem skorzystamy ze wzoru

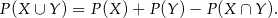
P(X ∪ Y) = P (X )+ P (Y) − P (X ∩ Y ).

Zauważmy, że 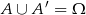A ∪ A ′ = Ω , więc

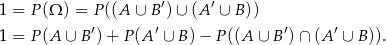
1 = P(Ω ) = P ((A ∪ B ′) ∪ (A ′ ∪ B)) ′ ′ ′ ′ 1 = P(A ∪ B )+ P (A ∪ B) − P ((A ∪ B ) ∩ (A ∪ B)).

Zatem

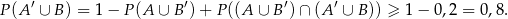
′ ′ ′ ′ P(A ∪ B ) = 1 − P (A ∪ B )+ P((A ∪ B )∩ (A ∪ B )) ≥ 1− 0,2 = 0,8.

Sposób III

Z diagramu widać, że

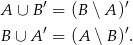
′ ′ A ∪ B = (B ∖ A ) B ∪ A ′ = (A ∖B )′.

Wiemy zatem, że

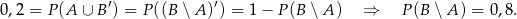
0 ,2 = P(A ∪ B′) = P((B ∖ A )′) = 1− P(B ∖ A) ⇒ P(B ∖ A ) = 0,8.

Mamy natomiast udowodnić, że

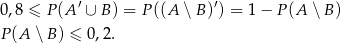
0 ,8 ≤ P(A ′ ∪ B ) = P((A ∖B )′) = 1− P(A ∖ B) P (A ∖ B) ≤ 0 ,2.

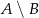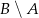To jednak jest oczywiste, bo zbiory A ∖B i B ∖A są rozłączne, czyli

1 ≥ P(A ∖B )+ P (B ∖ A) 1 ≥ P(A ∖B )+ 0 ,8 0,2 ≥ P(A ∖B ).
Wersja PDF