Zadanie nr 5689265
W urnie jest 2 razy więcej kul czarnych niż białych i 3 razy więcej kul zielonych niż białych. Przy losowaniu 3 kul z tej urny prawdopodobieństwo wylosowania 3 kul różnych kolorów wynosi 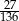 . Jakie jest prawdopodobieństwo wylosowania z urny 3 kul, wśród których dokładnie 2 będą tego samego koloru.
. Jakie jest prawdopodobieństwo wylosowania z urny 3 kul, wśród których dokładnie 2 będą tego samego koloru.
Rozwiązanie
Za zdarzenia elementarne przyjmijmy nieuporządkowane trójki wylosowanych kul. Oznaczmy liczbę kul białych przez  . Wtedy kul czarnych jest
. Wtedy kul czarnych jest 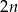 a kul zielonych
a kul zielonych 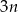 . Mamy zatem
. Mamy zatem
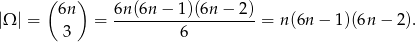
Zdarzeń, w których wylosowane kule są różne jest
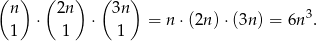
Mamy zatem
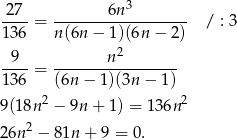
Stąd 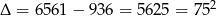 i jedyne całkowite rozwiązanie to
i jedyne całkowite rozwiązanie to 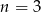 .
.
Możemy teraz policzyć szukane prawdopodobieństwo. Zdarzenia sprzyjające są trzech typów – w zależności od tego jaki jest kolor dwóch identycznych kul. Wszystkich zdarzeń sprzyjających jest
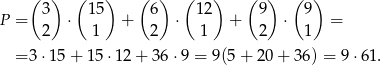
Mamy ponadto
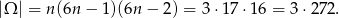
Stąd
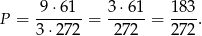
Odpowiedź: