Zadanie nr 5809699
Oblicz prawdopodobieństwo tego, że losowo wybrana liczba trzycyfrowa ma cyfrę setek mniejszą od cyfry dziesiątek, a cyfrę jedności równą cyfrze setek.
Rozwiązanie
Liczbę trzycyfrową możemy wybrać na
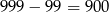
sposobów. Obliczmy teraz ile jest zdarzeń sprzyjających – szukamy liczb postaci 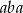 , gdzie
, gdzie 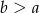 .
.
Sposób I
Cyfry  i
i 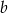 możemy wybrać na
możemy wybrać na
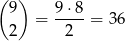
sposobów (po wybraniu dwóch różnych cyfr ustalamy, że  jest mniejszą, a
jest mniejszą, a 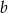 większą), więc interesujące nas prawdopodobieństwo jest równe
większą), więc interesujące nas prawdopodobieństwo jest równe
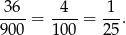
Sposób II
Zauważmy, że są
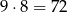
możliwości wybrania pary 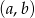 dwóch różnych niezerowych cyfr. Jednak tylko połowa z tych par spełnia warunek
dwóch różnych niezerowych cyfr. Jednak tylko połowa z tych par spełnia warunek 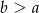 , więc interesujące nas prawdopodobieństwo jest równe
, więc interesujące nas prawdopodobieństwo jest równe
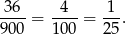
Sposób III
Wypisujemy liczby spełniające warunki zadania

Tych liczb jest
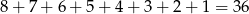
i interesujące nas prawdopodobieństwo jest równe
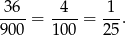
Odpowiedź: