Zadanie nr 6141118
Z pudełka, w którym jest 15 kul ponumerowanych kolejnymi liczbami od 1 do 15, losujemy bez zwracania 5 kul. Oblicz, jakie jest prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna para kul z sumą numerów równą 16.
Rozwiązanie
Wszystkich zdarzeń elementarnych jest
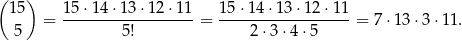
Wypiszmy wszystkie pary różnych liczb, które w sumie dają 16.
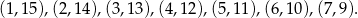
Jest jeszcze liczba 8, która nie ma pary (bo losujemy bez zwracania).
Sposób I
O zdarzeniach sprzyjających myślimy następująco: musimy wybrać jedną z powyższych par, a potem musimy dobrać jeszcze trzy liczby tak, aby nie były z jednej pary.
Jedną parę możemy wybrać na 7 sposobów. Po wybraniu tej pary pozostaje 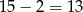 liczb i z nich musimy wybrać jeszcze trzy. Trzy pozostałe liczby możemy wybrać na
liczb i z nich musimy wybrać jeszcze trzy. Trzy pozostałe liczby możemy wybrać na
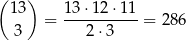
sposobów. Część z tych trójek będzie jednak zła – obliczmy ile takich jest. W ’złej trójce’ musi być para liczb z sumą 16 (którą już teraz możemy wybrać tylko na 6 sposobów!) oraz jedna dodatkowa liczba. Jest więc
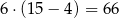
takich trójek. W takim razie wybraną na początku parę można uzupełnić do piątki na
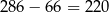
sposobów. W sumie jest więc
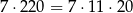
zdarzeń sprzyjających i prawdopodobieństwo jest równe
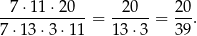
Sposób II
O zdarzeniach sprzyjających myślimy następująco: musimy wybrać jedną z powyższych par, a potem musimy dobrać jeszcze trzy liczby tak, aby nie były z jednej pary.
Jedną parę możemy wybrać na 7 sposobów. Gdy para ta jest ustalona to możliwe są dwie sytuacje: albo jedną z pozostałych liczb jest 8, albo nie.
Jeżeli jest 8 wśród wylosowanych liczb to pozostałe dwie liczby wybieramy następująco: wybieramy dwie pary, z których będą pochodzić te liczby – możemy to zrobić na
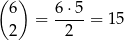
sposobów. Gdy te pary są już wybrane, to z każdej pary wybieramy jedną z dwóch liczb. Jest więc
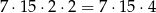
takich układów.
Jeżeli natomiast wśród wylosowanych liczb nie ma 8, to liczymy podobnie, najpierw wybieramy trzy pary, z których będą pochodzić pozostałe 3 liczby, a potem z każdej pary wybieramy jedną liczbę. Można to zrobić na
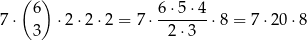
sposobów.
Prawdopodobieństwo jest więc równe
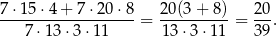
Sposób III
Tym razem, zamiast obliczać prawdopodobieństwo opisanego zdarzenia 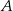 , obliczymy prawdopodobieństwo zdarzenia przeciwnego
, obliczymy prawdopodobieństwo zdarzenia przeciwnego 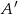 . Są dwa rodzaje zdarzeń sprzyjających zdarzeniu
. Są dwa rodzaje zdarzeń sprzyjających zdarzeniu 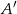 : albo nie ma żadnej pary z sumą równą 16, albo takie pary są dwie.
: albo nie ma żadnej pary z sumą równą 16, albo takie pary są dwie.
Łatwo obliczyć liczbę zdarzeń z dwoma parami z sumą równą 16 – wybieramy dwie pary spośród 7 par z sumą równą 16, a potem dobieramy 5-tą liczbę dowolnie spośród 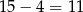 pozostałych liczb. Jest więc
pozostałych liczb. Jest więc
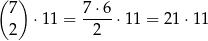
zdarzeń tego typu.
Jeżeli natomiast nie ma żadnej pary liczb z sumą równą 16, to każda z liczb musi pochodzić z innej z wypisanych par, lub może być też 8-ką.
Jeżeli wśród wybranych liczb jest 8, to aby wybrać pozostałe cztery liczby wybieramy 4 pary, z których będą pochodzić. Możemy to zrobić na
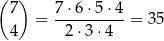
sposobów. Ponadto w każdej z 4 wybranych par możemy wybrać jedną z dwóch liczb. Jest więc
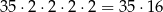
takich par.
Jeżeli wreszcie wśród wybranych liczb nie ma 8-ki, to liczby pochodzą z 5 różnych par, które możemy wybrać na
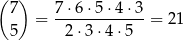
sposobów. W każdej parze mamy możliwość wyboru jednej z 2 liczb. Jest więc
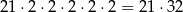
takich zdarzeń.
Prawdopodobieństwo jest więc równe.
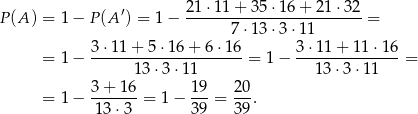
Odpowiedź: