Zadanie nr 6165467
Ze zbioru liczb naturalnych pięciocyfrowych wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 15.
Rozwiązanie
Ile jest liczb naturalnych i pięciocyfrowych? – od 99999 liczb co najwyżej pięciocyfrowych trzeba odjąć 9999 czterocyfrowych. Zatem
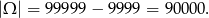
Ile jest liczb podzielnych przez 15? – najmniejsza to
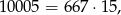
a największa to
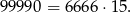
Jest więc tych liczb tyle, co liczb pomiędzy 667 a 6666, czyli
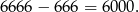
Zatem szukane prawdopodobieństwo wynosi
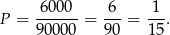
Odpowiedź: