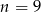Zadanie nr 6256414
Ze zbioru liczb 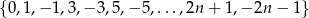 , gdzie
, gdzie  jest ustaloną liczbą naturalną, większą od 4, losujemy jednocześnie trzy liczby. Niech
jest ustaloną liczbą naturalną, większą od 4, losujemy jednocześnie trzy liczby. Niech 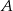 oznacza zdarzenie: suma wylosowanych liczb nie ulegnie zmianie, jeżeli w wylosowanych liczbach zmienimy znaki na przeciwne. Wiedząc, że
oznacza zdarzenie: suma wylosowanych liczb nie ulegnie zmianie, jeżeli w wylosowanych liczbach zmienimy znaki na przeciwne. Wiedząc, że 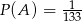 , oblicz
, oblicz  .
.
Rozwiązanie
Policzmy ile jest liczb w danym zbiorze. Ponieważ
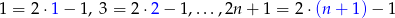
tych liczb jest 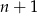 . W całym zbiorze jest więc
. W całym zbiorze jest więc 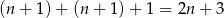 liczb. Zatem możliwości wybrania trzech z nich jest
liczb. Zatem możliwości wybrania trzech z nich jest
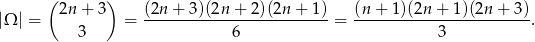
Jeżeli 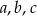 są trzema wylosowanymi liczbami, to przy zmianie ich znaków, suma nie zmieni się wtedy i tylko wtedy, gdy
są trzema wylosowanymi liczbami, to przy zmianie ich znaków, suma nie zmieni się wtedy i tylko wtedy, gdy 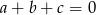 . Jest jednak mały problem, w danym zbiorze jest tylko jedna liczba parzysta, a w równości
. Jest jednak mały problem, w danym zbiorze jest tylko jedna liczba parzysta, a w równości 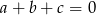 nie mogą wszystkie trzy liczby być nieparzyste. Zatem jedna z tych liczb, powiedzmy
nie mogą wszystkie trzy liczby być nieparzyste. Zatem jedna z tych liczb, powiedzmy  jest równa 0. Mamy w takim razie równość
jest równa 0. Mamy w takim razie równość 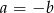 . Ile jest takich par? – to łatwe, tyle ile jest liczb dodatnich w danym zbiorze, czyli
. Ile jest takich par? – to łatwe, tyle ile jest liczb dodatnich w danym zbiorze, czyli 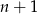 . Interesujące nas prawdopodobieństwo jest więc równe
. Interesujące nas prawdopodobieństwo jest więc równe
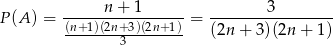
(bo nie uwzględniamy kolejności losowania liczb).
Mamy zatem równanie
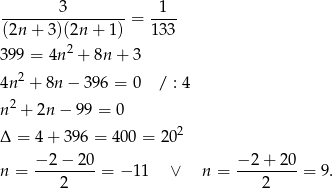
Ujemne rozwiązanie odrzucamy i mamy 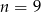 .
.
Odpowiedź: