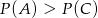/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 6441024

Dodaj do ulubionych
Dodaj do rozwiązanych

W urnie znajduje się 40 losów, wśród których są tylko losy wygrywające i przegrywające. Z urny wyciągamy dwa losy. Niech 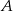A oznacza zdarzenie – wylosowano dwa losy wygrywające, zaś 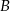B zdarzenie – wylosowano jeden los wygrywający i jeden przegrywający.

  • Oblicz ile jest losów wygrywających, jeżeli P (A ) = P(B ) .
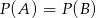  • Sprawdź, które zdarzenie jest bardziej prawdopodobne: zdarzenie 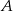A , czy zdarzenie 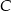C – wylosowano dwa losy przegrywające

Rozwiązanie

Za zdarzenia elementarne przyjmijmy dwuelementowe zbiory wylosowanych losów. Zatem

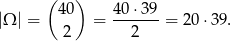
( ) |Ω | = 40 = 40⋅-39-= 20 ⋅39. 2 2
  • Oznaczmy liczbę losów wygrywających przez n . Zatem dwa losy wygrywające można wybrać na
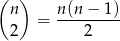
    ( ) n n (n− 1) = --------- 2 2

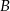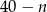    sposoby. Policzmy jeszcze liczbę zdarzeń sprzyjających zdarzeniu B : los wygrywający możemy wybrać na n sposobów, a przegrywający na 4 0− n sposobów. Zatem jest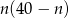

    n(40 − n)

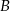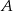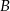    zdarzeń sprzyjających zdarzeniu B . Skoro zdarzenia A i B są jednakowo prawdopodobne, liczby zdarzeń sprzyjających muszą być równe (specjalnie porównujemy je, nie prawdopodobieństwa, żeby nie pisać mianowników, które i tak się skrócą). Mamy więc równanie.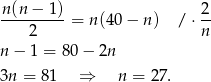

    n (n− 1) 2 --------- = n (40− n) / ⋅ -- 2 n n − 1 = 8 0− 2n 3n = 81 ⇒ n = 27.

     
    Odpowiedź: 27

  • Z poprzedniego podpunktu wiemy, że jest więcej losów wygrywających niż przegrywających. Zatem łatwiej wylosować dwa losy wygrywające, niż dwa losy przegrywające.

    Jeżeli to kogoś nie przekonuje to możemy policzyć odpowiednie liczby zdarzeń sprzyjających:

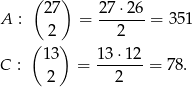
    ( ) A : 27 = 27-⋅26-= 3 51 2 2 ( ) C : 13 = 13⋅1-2-= 78. 2 2

     
    Odpowiedź: P(A ) > P (C)

Wersja PDF