/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 6597926

Dodaj do ulubionych
Dodaj do rozwiązanych

Rzucamy pięć razy symetryczną monetą. Po przeprowadzonym doświadczeniu zapisujemy liczbę uzyskanych orłów (od 0 do 5) i liczbę uzyskanych reszek (również od 0 do 5). Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tych pięciu rzutach liczba uzyskanych orłów będzie mniejsza niż liczba uzyskanych reszek.

Rozwiązanie

Sposób I

W każdym rzucie mamy dwa możliwe wyniki, więc jest

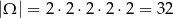
|Ω | = 2 ⋅2 ⋅2 ⋅2⋅2 = 32

wszystkich możliwych zdarzeń. Wypisujemy teraz zdarzenia sprzyjające

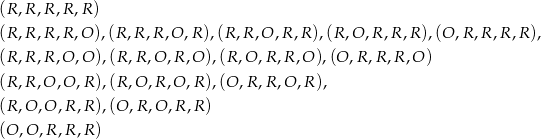
(R,R ,R ,R,R ) (R,R ,R ,R,O ),(R,R ,R ,O,R ),(R,R ,O ,R,R ),(R,O ,R ,R,R ),(O ,R,R ,R,R ), (R,R ,R ,O,O ),(R ,R,O ,R,O ),(R ,O,R ,R ,O),(O ,R ,R,R ,O ) (R,R ,O ,O,R ),(R ,O,R ,O ,R),(O ,R,R ,O ,R), (R,O ,O ,R,R ),(O ,R,O ,R ,R) (O ,O,R ,R,R )

Jest więc 16 zdarzeń sprzyjających i interesujące nas prawdopodobieństwo jest więc równe

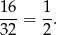
16- 1- 32 = 2.

Sposób II

Ponieważ orły i reszki pełnią takie same role w przeprowadzanym doświadczeniu, jest tyle samo darzeń, w których orłów jest więcej niż reszek, jak zdarzeń w których reszek jest więcej niż orłów. Z drugiej strony, liczba rzutów jest nieparzysta, więc zawsze zachodzi jedna z dwóch wymienionych sytuacji. To oznacza, że prawdopodobieństwo interesującego nas zdarzenia musi być równe 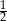12 .  
Odpowiedź: 1 2

Wersja PDF