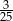Zadanie nr 7113835
Ze zbioru 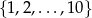 losujemy kolejno 3 liczby (mogą się powtarzać). Wyznacz prawdopodobieństwo wyboru takiej trójki
losujemy kolejno 3 liczby (mogą się powtarzać). Wyznacz prawdopodobieństwo wyboru takiej trójki 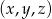 liczb, dla której
liczb, dla której 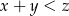 .
.
Rozwiązanie
Sposób I
Możliwości wylosowania trzech liczb jest
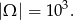
Policzmy ile jest zdarzeń sprzyjających.
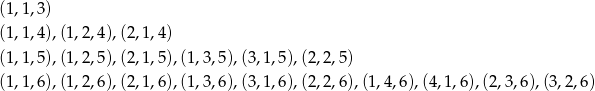
i tak dalej – wypisywanie zaczyna już być niewygodne, więc spróbujmy to zrobić trochę mądrzej. Zauważmy, że jak trójka 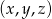 jest dobra to trójka
jest dobra to trójka 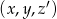 też jest dobra dla
też jest dobra dla 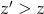 . Spróbujemy więc teraz wypisać tylko te trójki
. Spróbujemy więc teraz wypisać tylko te trójki 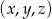 dla których trójka
dla których trójka 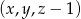 jest zła – wypisujemy tylko nowe pary
jest zła – wypisujemy tylko nowe pary 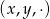 .
.

Innymi słowy, jeżeli 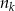 jest liczbą trójek takich, że
jest liczbą trójek takich, że 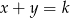 to
to 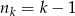 . Ile jest zdarzeń sprzyjających? Dla ustalonego
. Ile jest zdarzeń sprzyjających? Dla ustalonego  jest ich
jest ich 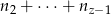 , czyli w sumie mamy
, czyli w sumie mamy
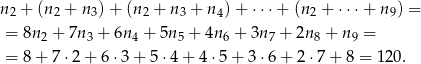
Zatem prawdopodobieństwo wynosi
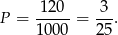
Sposób II
Mądrzejsi o rachunki z poprzedniego podpunktu, możemy obyć się bez wypisywania zdarzeń. Jak poprzednio oznaczmy przez 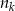 liczbę par
liczbę par 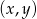 o sumie
o sumie 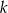 . Ponieważ
. Ponieważ  możemy wybrać na
możemy wybrać na 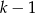 sposobów, a
sposobów, a 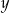 jest jednoznacznie wyznaczony przez
jest jednoznacznie wyznaczony przez  , mamy
, mamy 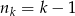 . Ile jest zdarzeń sprzyjających
. Ile jest zdarzeń sprzyjających 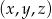 , w których
, w których 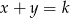 ? – jest ich
? – jest ich 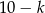 , bo na tyle sposobów można dobrać
, bo na tyle sposobów można dobrać  . Razem mamy zatem (biorąc
. Razem mamy zatem (biorąc 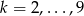 )
)
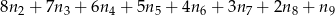
zdarzeń sprzyjających. Dalej liczymy jak poprzednio.
Odpowiedź: