/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 7183218

Dodaj do ulubionych
Dodaj do rozwiązanych

Do koszyka włożono 12 jabłek, w tym dwa jabłka lobo. Po kilku dniach przechowywania z koszyka usunięto dwa popsute jabłka. Następnie losowo wybrano jedno jabłko. Oblicz prawdopodobieństwo, że wybrano jabłko lobo. Wynik podaj w postaci ułamka nieskracalnego.

Rozwiązanie

Sposób I

Usuwając dwa popsute jabłka mogła się zdarzyć jedna z trzech sytuacji: mogliśmy usunąć dwa jabłka lobo, mogliśmy usunąć jedno jabłko lobo i jedno inne jabłko, mogliśmy wreszcie usunąć dwa jabłka inne niż lobo. Jeżeli oznaczymy te zdarzenia odpowiednio przez 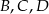B,C ,D to mamy

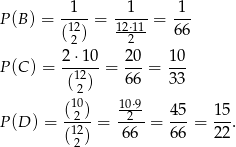
1 1 1 P(B ) = -12- = -12⋅11 = --- ( 2) 2 66 2-⋅10- 20- 10- P(C ) = 12 = 66 = 33 (2 ) (10) 10⋅9- 45 15 P(D ) = -212--= -2--= ---= ---. (2) 66 66 22

Jeżeli teraz oznaczymy interesujące nas prawdopodobieństwo wybrania jabłka lobo przez 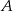A , to ze wzoru na prawdopodobieństwo całkowite (lub z drzewka) mamy

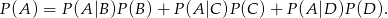
P (A ) = P(A |B)P (B) + P (A|C )P(C )+ P(A |D )P(D ).

Obliczmy powyższe prawdopodobieństwa warunkowe.

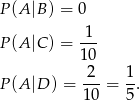
P (A |B ) = 0 P (A |C ) = -1- 1 0 2 1 P (A |D ) = ---= -. 10 5

Mamy zatem

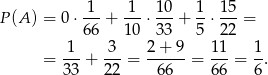
-1- 1-- 10- 1- 15- P(A ) = 0 ⋅66 + 10 ⋅33 + 5 ⋅ 22 = 1 3 2+ 9 1 1 1 = ---+ ---= ------= --- = --. 33 22 66 6 6 6

Sposób II

O całej sytuacji możemy myśleć trochę inaczej: wybieramy z koszyka trzy jabłka, a potem z tych trzech jedno (pozostałe dwa są popsute). Twierdzimy, że prawdopodobieństwo otrzymania w ten sposób jabłka lobo jest dokładnie takie samo, jak w przypadku zdarzenia 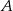A polegającego na wylosowaniu jednego jabłka spośród wszystkich dwunastu, tzn. jest równe

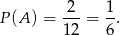
-2- 1- P(A ) = 1 2 = 6 .

Rzeczywiście, jeżeli przez 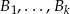B1,...,Bk oznaczymy wszystkie możliwe zdarzenia polegające na wybraniu 3 jabłek z koszyka to ze wzoru na prawdopodobieństwo całkowite mamy

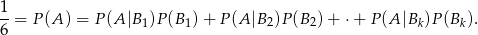
1-= P(A ) = P (A |B )P(B )+ P (A |B )P(B )+ ⋅+ P (A|B )P (B ). 6 1 1 2 2 k k

Zauważmy teraz, że prawa strona tej równości to dokładnie prawdopodobieństwo interesującego nas zdarzenia, tzn. zdarzenia polegającego na wybraniu najpierw 3 jabłek, a potem jednego.  
Odpowiedź: 16

Wersja PDF