/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 7211755

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru 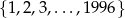{1,2,3,...,1996 } losujemy jedną liczbę. Oblicz prawdopodobieństwo, że wylosowana liczba jest podzielna przez:

  • 6
  • 4 lub 6
  • 4 lub 6 lub 10

Rozwiązanie

  • Aby obliczyć szukane prawdopodobieństwo, sprawdźmy ile liczb dzieli się przez 6
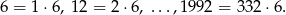
    6 = 1 ⋅6, 12 = 2 ⋅6, ...,1992 = 3 32⋅6 .

    Mamy zatem

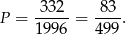
    P = 3-32-= -83-. 1996 499

     
    Odpowiedź: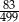 83- 499

  • Podobnie jak poprzednio, policzmy liczby podzielne przez 4.
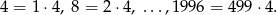
    4 = 1⋅ 4, 8 = 2⋅4 , ...,1996 = 499 ⋅4.

    Aby obliczyć ilość liczb podzielnych przez 4 lub 6 nie wystarczy dodać ilości liczb podzielnych przez 4 i przez 6, bo liczby podzielne przez obie z nich, czyli przez 12, policzymy podwójnie. Policzmy ile liczb dzieli się przez 12.

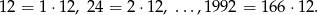
    12 = 1 ⋅12, 24 = 2 ⋅12, ...,1992 = 166⋅ 12.

    Mamay zatem

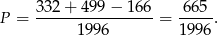
    P = 332+--499-−-166-= -665-. 19 96 199 6

     
    Odpowiedź: 665- 1996

  • Policzymy jak poprzednio, ale ponieważ mamy teraz trzy liczby, skorzystamy ze wzoru
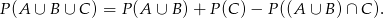
    P (A ∪ B ∪ C ) = P(A ∪ B) + P (C ) − P((A ∪ B) ∩ C).

    Wzór ten łatwo uzasadnić sobie na obrazku, jest to zresztą szczególny przypadek znanego wzoru

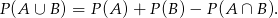
    P (A ∪ B ) = P(A ) + P (B)− P(A ∩ B).

    W naszym przypadku
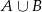    A ∪ B : liczby podzielne przez 4 lub 6
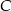    C : liczby podzielne przez 10
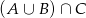    (A ∪ B )∩ C : liczby podzielne przez 4 lub 6 i przez 10, czyli przez 20 lub 30.
    Aby policzyć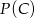 P(C ) , liczymy ilość liczb podzielnych przez 10.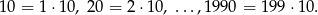

    10 = 1 ⋅10, 20 = 2 ⋅10, ...,1990 = 199⋅ 10.

    Zatem

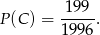
    199 P(C ) = -----. 199 6

    Liczby podzielne przez 20 lub 30 liczymy jak w poprzednim podpunkcie

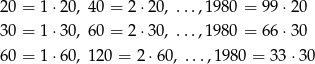
    20 = 1 ⋅20 , 40 = 2 ⋅20 , ...,1980 = 99 ⋅20 30 = 1 ⋅30 , 60 = 2 ⋅30 , ...,1980 = 66 ⋅30 60 = 1 ⋅60 , 120 = 2⋅6 0, ...,198 0 = 33 ⋅30

    Tak więc

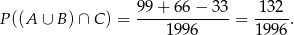
    P ((A ∪ B )∩ C ) = 99-+-66-−-3-3 = -132-. 199 6 19 96

    I dalej

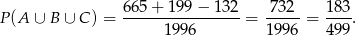
    665 + 19 9− 1 32 732 183 P (A ∪ B ∪ C ) = ---------------- = -----= ---. 1996 1996 499

     
    Odpowiedź: 183 499

Wersja PDF