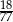/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 7254028

Dodaj do ulubionych
Dodaj do rozwiązanych

Grupę 12 uczniów, wśród których jest 6 dziewczynek i 6 chłopców podzielono na 3 równoliczne grupy. Oblicz prawdopodobieństwo tego, że w każdej z utworzonych grup będzie tyle samo dziewcząt.

Rozwiązanie

Opisany podział to tak naprawdę wybór 4 uczniów, którzy się znajdą w pierwszej grupie oraz wybór 4 uczniów z pozostałej 8-ki, którzy znajdą się w drugiej grupie. Po dokonaniu tych wyborów skład 3 grupy jest już jednoznacznie wyznaczony. Mamy zatem

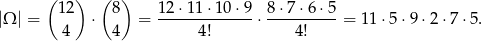
( ) ( ) 12 8 12-⋅11⋅-10⋅9- 8⋅7-⋅6-⋅5- |Ω | = 4 ⋅ 4 = 4! ⋅ 4 ! = 1 1⋅5 ⋅9 ⋅2⋅ 7⋅5 .

W zdarzeniach sprzyjających musimy wybrać 2 dziewczynki do pierwszej grupy oraz 2 towarzyszących im chłopców. Potem z pozostałych 4 dziewcząt i 4 chłopców wybieramy po dwie osoby do drugiej grupy. Po dokonaniu tych wyborów skład 3 grupy jest już jednoznacznie ustalony. Jest więc

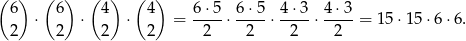
( 6) ( 6) ( 4) (4) 6⋅5 6⋅5 4⋅3 4 ⋅3 ⋅ ⋅ ⋅ = ----⋅ ----⋅ ----⋅---- = 15 ⋅15⋅ 6⋅6. 2 2 2 2 2 2 2 2

Prawdopodobieństwo jest więc równe

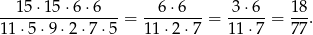
--15-⋅15⋅-6⋅6----= --6-⋅6-- = 3-⋅6--= 1-8. 11⋅ 5⋅9 ⋅2 ⋅7⋅ 5 11 ⋅2 ⋅7 11⋅ 7 7 7

 
Odpowiedź: 18 77

Wersja PDF