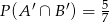Zadanie nr 7374529
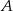 i
i 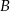 są takim zdarzeniami losowymi zawartymi w
są takim zdarzeniami losowymi zawartymi w 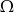 , że
, że 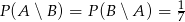 i
i 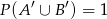 . Oblicz
. Oblicz 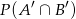 .
.
Rozwiązanie
Rozpoczynamy od naszkicowania diagramu Venna.
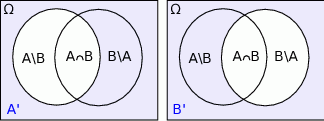
Sposób I
Zauważmy, że 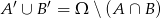 . Zatem z podanej informacji
. Zatem z podanej informacji 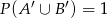 wynika, że
wynika, że
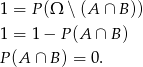
Zatem 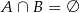 . Wynika stąd, że
. Wynika stąd, że
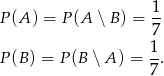
Ponownie patrzymy na diagram Venna i odczytujemy, że 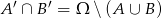 . Stąd
. Stąd
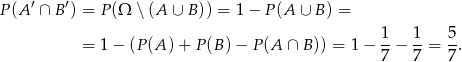
Po drodze skorzystaliśmy ze wzoru na prawdopodobieństwo sumy zdarzeń.
Sposób II
Zauważmy, ze równość 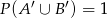 oznacza, że każde zdarzenie jest poza
oznacza, że każde zdarzenie jest poza 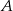 lub poza
lub poza 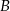 . To oznacza, że nie ma zdarzeń, które są jednocześnie w
. To oznacza, że nie ma zdarzeń, które są jednocześnie w 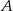 i
i 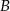 . Zatem
. Zatem 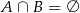 i
i
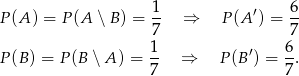
Znamy 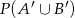 , a mamy obliczyć
, a mamy obliczyć 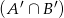 , korzystamy więc ze wzoru na prawdopodobieństwo sumy zdarzeń.
, korzystamy więc ze wzoru na prawdopodobieństwo sumy zdarzeń.
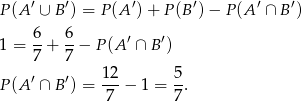
Sposób III
Korzystamy z praw De Morgana (które łatwo odczytać z diagramu Venna).
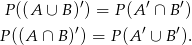
W naszej sytuacji mamy
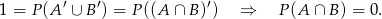
Zatem 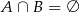 i
i
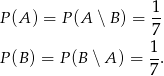
Stąd
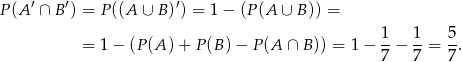
Odpowiedź: