Zadanie nr 7386315
W urnie znajdują się kule czarne, białe i niebieskie, przy czym są co najmniej dwie kule każdego koloru i w sumie jest 15 kul. Losujemy z urny trzy kule. Rozważmy następujące zdarzenia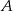 
– wylosowano trzy kule tego samego koloru;
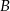– żadne dwie z wylosowanych kul nie są tego samego koloru.
Oblicz prawdopodobieństwo zdarzenia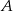 
jeżeli prawdopodobieństwo zdarzenia 
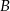jest równe 
.
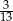Rozwiązanie
W rozwiązaniu będziemy kilka razy liczyć symbol Newtona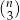 
, więc od razu ustalmy, że jest on równy
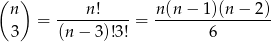
(skraca się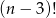 
).
Oznaczmy liczby kul każdego z kolorów przez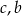 
i 
odpowiednio. Trzy kule możemy wybrać na
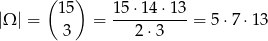
sposobów.
Zastanówmy się teraz nad zdarzeniem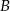 
. Ile jest trójek, w których każda kula ma inny kolor? – jest ich 
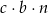. Mamy więc równanie
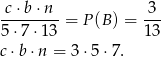
Teraz musimy skorzystać z faktu, że są co najmniej dwie kule każdego koloru, czyli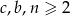 
. Prawą stronę powyższej równości można napisać dokładnie w jeden sposób jako iloczyn trzech liczb całkowitych większych od 1, więc liczby 
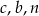muszą być równe 3,5,7 (w pewnej kolejności). Mówiąc jeszcze inaczej, ile może być równe 
? – musi dzielić prawą stronę i nie może być iloczynem dwóch z wypisanych tam liczb, bo wtedy nie da się dobrać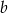 
i 
, zatem 
musi być jedną z liczb 3,5,7. Podobnie z pozostałymi liczbami.
Zobaczmy teraz co mamy policzyć. Jeżeli kule mają być tego samego koloru, to mogą być wszystkie czarne, wszystkie białe lub wszystkie niebieskie. W sumie jest więc
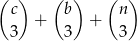
takich układów. Wprawdzie nie wiemy dokładnie, która z liczb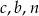 
jest równa 3, która 5, a która 7, ale przy obliczaniu powyższego wyrażenia nie ma to znaczenia – w każdej konfiguracji wyjdzie dokładnie ten sam wynik:
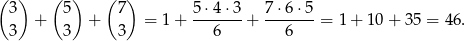
Zatem szukane prawdopodobieństwo jest równe
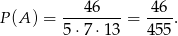
Odpowiedź: 
