Zadanie nr 7656542
Wśród 150 mieszkańców pewnego osiedla przeprowadzono ankietę. Zadano pytanie, z jakiej sieci telefonii komórkowej korzystają. Wyniki badania przedstawiono w tabeli:
| Sieć | Ile osób korzysta |
| „Krzyżyk” | 75 |
| „Kółko” | 60 |
Okazało się, że wśród ankietowanych, 10 osób posiada telefony w obydwu sieciach. Oblicz prawdopodobieństwo, że losowo wybrana osoba spośród ankietowanych nie posiada telefonu w żadnej z wymienionych sieci. Wynik przedstaw w formie nieskracalnego ułamka.
Rozwiązanie
Sposób I
Niech 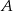 oznacza zbiór osób, które korzystają z sieci „Krzyżyk”, a
oznacza zbiór osób, które korzystają z sieci „Krzyżyk”, a 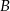 zbiór osób, które korzystają z sieci „Kółko”. Wiemy zatem, że
zbiór osób, które korzystają z sieci „Kółko”. Wiemy zatem, że 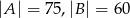 oraz
oraz 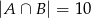 . To pozwala obliczyć ile osób korzysta z jednej z tych sieci
. To pozwala obliczyć ile osób korzysta z jednej z tych sieci
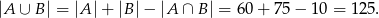
Wszystkich mieszkańców jest 150, więc osób, które nie korzystają z tych dwóch sieci jest
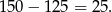
Szukane prawdopodobieństwo jest więc równe
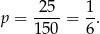
Sposób II
Oznaczmy przez 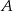 i
i 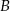 zdarzenia polegające na tym, że losowo wybrana osoba korzysta odpowiednio z sieci „Krzyżyk” i „Kółko”. Wiemy zatem, że
zdarzenia polegające na tym, że losowo wybrana osoba korzysta odpowiednio z sieci „Krzyżyk” i „Kółko”. Wiemy zatem, że 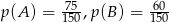 oraz
oraz 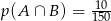 . Mamy natomiast obliczyć prawdopodobieństwo
. Mamy natomiast obliczyć prawdopodobieństwo 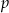 zdarzenia przeciwnego do
zdarzenia przeciwnego do 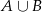 . Mamy zatem
. Mamy zatem
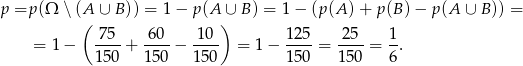
Odpowiedź: 

