Zadanie nr 7836920
Oblicz prawdopodobieństwo tego, że dwa losowo wybrane wierzchołki sześciokąta foremnego o boku długości 1, są końcami odcinka o długości 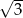 .
.
Rozwiązanie
Naszkicujmy sobie taki sześciokąt.
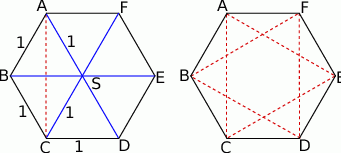
Składa się on z 6 przystających trójkątów równobocznych o boku długości 1. Ponieważ wysokość takiego trójkąta ma długość 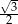 odcinki, o których mowa w treści zadania, to krótsze przekątne sześciokąta.
odcinki, o których mowa w treści zadania, to krótsze przekątne sześciokąta.
Sposób I
Ile jest odcinków o końcach w wierzchołkach sześciokąta? Jest 6 boków, 3 długie przekątne i 6 krótszych przekątnych. Zatem szukane prawdopodobieństwo wynosi
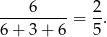
Sposób II
Jeżeli wolimy znaczki od zdrowego rozsądku, to przyjmijmy, że zdarzenia elementarne to dwuelementowe zbiory wylosowanych wierzchołków, czyli
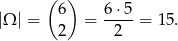
Ile jest zdarzeń sprzyjających? – z każdego wierzchołka wychodzą dwie krótsze przekątne, czyli jest ich 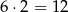 . No, prawie tyle, bo każdą policzyliśmy dwa razy (w obu końcach), więc jest ich
. No, prawie tyle, bo każdą policzyliśmy dwa razy (w obu końcach), więc jest ich 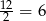 . Daje nam to prawdopodobieństwo
. Daje nam to prawdopodobieństwo
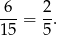
Odpowiedź: 

