Zadanie nr 8408364
Rzucamy dwa razy symetryczną, sześcienną kostką, której jedna ściana ma jedno oczko, dwie ściany mają po dwa oczka i trzy ściany mają po trzy oczka. Oblicz prawdopodobieństwo zdarzenia: liczby oczek otrzymane w obu rzutach różnią się o 1.
Rozwiązanie
Za zdarzenia elementarne przyjmijmy pary wyrzuconych ścianek, czyli
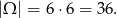
Są 4 rodzaje zdarzeń sprzyjających: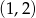
– taką parę możemy otrzymać na 
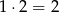sposoby.
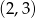– taką parę możemy otrzymać na 
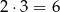sposobów.
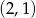– taką parę możemy otrzymać na 
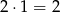sposoby.
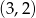– taką parę możemy otrzymać na 
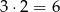sposobów.
Zatem prawdopodobieństwo wynosi
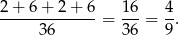
Odpowiedź: 
