Zadanie nr 8448801
Dany jest ciąg 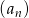 o wyrazie ogólnym
o wyrazie ogólnym 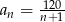 , dla każdej liczby naturalnej
, dla każdej liczby naturalnej 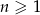 . Ze zbioru liczb
. Ze zbioru liczb 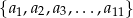 losujemy kolejno, trzy razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno, trzy razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 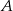 – wylosujemy trzy liczby całkowite, które będą kolejnymi wyrazami ciągu malejącego.
– wylosujemy trzy liczby całkowite, które będą kolejnymi wyrazami ciągu malejącego.
Rozwiązanie
Na początku wypiszmy zbiór liczb z którego losujemy (dzielimy 120 przez 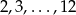 )
)
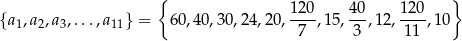
Jeżeli za zdarzenia elementarne przyjmiemy uporządkowane trójki wylosowanych liczb, to mamy
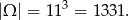
Jaki są zdarzenia sprzyjające? – są to dokładnie malejące trójki liczb całkowitych w powyższym zbiorze. Wszystkich liczb całkowitych jest 8, więc takich trójek jest
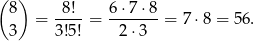
Zatem szukane prawdopodobieństwo wynosi
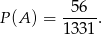
Odpowiedź: