/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 8678297

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz prawdopodobieństwo warunkowe, że w trzykrotnym rzucie symetryczną sześcienną kostką do gry otrzymamy co najmniej jedną „jedynkę”, pod warunkiem że otrzymamy co najmniej jedną „szóstkę”.

Rozwiązanie

Za zdarzenia elementarne przyjmijmy uporządkowane trójki wylosowanych oczek. Mamy więc

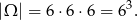
|Ω | = 6 ⋅6⋅ 6 = 63.

Niech 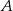A oznacza zdarzenie polegające na otrzymaniu co najmniej jednej jedynki, a 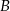B zdarzenie polegające na otrzymaniu co najmniej jednej szóstki. Musimy obliczyć

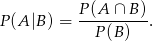
P (A ∩ B ) P (A |B ) = ----------. P(B )

Prawdopodobieństwo zdarzenia 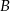B łatwo obliczyć jeżeli przejdziemy do zdarzenia przeciwnego 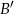′ B . Zdarzenia sprzyjające 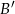′ B , to takie, w których na żadnej z kostek nie ma szóstki. Jest więc 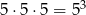5⋅5 ⋅5 = 5 3 takich zdarzeń i

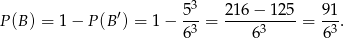
′ 5-3 216-−-1-25 9-1 P (B) = 1− P (B ) = 1 − 6 3 = 63 = 63.

Zdarzenia sprzyjające zdarzeniu 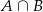A ∩ B (czyli otrzymaniu co najmniej jednej jedynki i co najmniej jednej szóstki) możemy podzielić na trzy typy:
– wylosowaliśmy 2 jedynki i 1 szóstkę – są trzy takie zdarzenia (szóstkę możemy otrzymać na jednej z trzech kostek);
– wylosowaliśmy 1 jedynkę i 2 szóstki – są trzy takie zdarzenia (jedynkę możemy otrzymać na jednej z trzech kostek);
– wylosowaliśmy 1 jedynkę, 1 szóstkę i jedną liczbę różną od 1 i 6 – takich zdarzeń jest 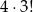4⋅3 ! (na 4 sposoby możemy wybrać trzecią liczbę i potem na 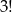3! sposobów możemy ustalić kolejność wybranych liczb).
Mamy więc

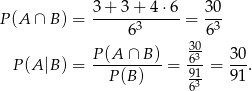
3 + 3 + 4 ⋅6 30 P(A ∩ B) = ------3----- = -3- 6 6 P (A ∩ B ) 3063- 30 P (A |B) = ---P(B-)-- = -91-= 91-. 63

 
Odpowiedź: 3901

Wersja PDF