/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 9118666

Dodaj do ulubionych
Dodaj do rozwiązanych

W dwunastu rzutach monetą cztery razy wypadł orzeł. Oblicz prawdopodobieństwo, że orzeł wypadł w piątym rzucie tej serii rzutów.

Rozwiązanie

Sposób I

Musimy obliczyć prawdopodobieństwo warunkowe

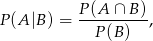
P (A ∩ B ) P (A |B ) = ----------, P(B )

gdzie zdarzenie 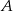A polega na wyrzuceniu orła w piątym rzucie, a zdarzenie 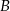B na otrzymaniu czterech orłów w 12 rzutach.

Prawdopodobieństwo 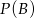P (B) liczymy wprost ze schematu Bernoulliego

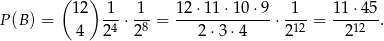
( ) 12 1-- 1-- 12⋅-11⋅-10⋅9- -1- 11-⋅45- P(B ) = 4 24 ⋅28 = 2⋅ 3⋅4 ⋅ 212 = 212 .

Pozostało policzyć prawdopodobieństwo 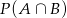P (A ∩ B ) . Można sobie o tym myśleć tak: w piątym rzucie ma wypaść orzeł, a w pozostałych 11 rzutach mają być 3 orły. Ponownie korzystamy ze schematu Bernoulliego.

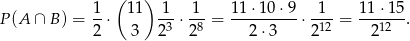
( ) P(A ∩ B) = 1⋅ 11 1-⋅ 1--= 1-1⋅1-0⋅9 ⋅-1- = 11-⋅15. 2 3 23 28 2 ⋅3 2 12 212

Zatem szukane prawdopodobieństwo wynosi

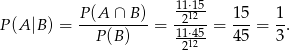
11⋅15 P (A|B ) = P(A--∩-B)-= -212-= 15-= 1. P (B) 11⋅4152 45 3 2

Sposób II

Oczywiście wyrzucenie orła w każdym z rzutów jest tak samo prawdopodobne. Zatem musi być równe 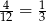4-= 1 12 3 (bo wiemy, że mają być cztery orły).  
Odpowiedź: 1 3

Wersja PDF