/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 9250920

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest wielomian 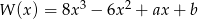3 2 W (x) = 8x − 6x + ax+ b . Jednym pierwiastkiem wielomianu jest prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.

Rozwiązanie

Obliczmy podane prawdopodobieństwa.

Jeżeli za zdarzenia sprzyjające przy trzykrotnym rzucie monetą przyjmiemy trójki otrzymanych stron monety, to mamy

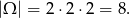
|Ω | = 2 ⋅2 ⋅2 = 8.

Wypiszmy zdarzenia, w których są co najmniej 2 orły:

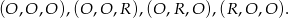
(O ,O ,O),(O ,O ,R),(O ,R ,O),(R ,O ,O).

Zatem prawdopodobieństwo wynosi 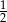1 2 .

Jeżeli za zdarzenia elementarne w rzucie dwoma kostkami przyjmiemy pary otrzymanych liczb oczek, to mamy

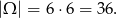
|Ω | = 6 ⋅6 = 36 .

Zdarzeń sprzyjających jest

3⋅3 = 9,

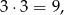
bo na każdej kostce może wypaść jedna z liczb: 2,4,6. Zatem prawdopodobieństwo jest równe 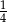1 4 .

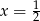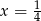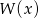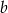Teraz mamy różne możliwości, możemy podstawić 1 x = 2 i 1 x = 4 do wzoru na W (x) i wyliczyć z tego a i b . Można też od razu podzielić wielomian 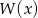W (x) przez

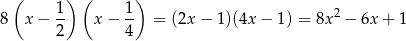
( ) ( ) 8 x − 1- x − 1- = (2x − 1)(4x − 1) = 8x 2 − 6x + 1 2 4

i zobaczyć kiedy reszta jest zero. W tym sposobie za darmo wyjdzie nam trzeci pierwiastek. My dzielimy grupując wyrazy.

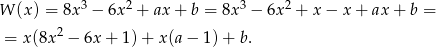
W (x ) = 8x3 − 6x2 + ax + b = 8x3 − 6x2 + x − x + ax + b = 2 = x (8x − 6x + 1)+ x(a − 1) + b.

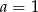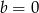Widać zatem, że reszta jest zero tylko dla a = 1 i b = 0 . Powyższa równość przyjmuje wtedy postać

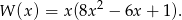
2 W (x) = x(8x − 6x+ 1).

Zatem trzeci pierwiastek to 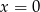x = 0 .  
Odpowiedź: x = 0

Wersja PDF