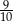/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 9424219

Dodaj do ulubionych
Dodaj do rozwiązanych

Z pojemnika, w którym znajduje się pięć kul: dwie białe i trzy czerwone, losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę czerwoną. Wynik przedstaw w postaci ułamka nieskracalnego.

Rozwiązanie

Sposób I

Parę kul możemy wybrać na

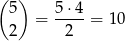
( ) 5 5-⋅4 2 = 2 = 1 0

sposobów. Ponadto jest dokładnie jedno zdarzenie, w którym nie ma kuli czerwonej (tzn. są dwie kule białe), więc interesujące nas prawdopodobieństwo jest równe

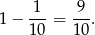
1 9 1 − ---= ---. 10 1 0

Sposób II

Tym razem za zdarzenia sprzyjające przyjmijmy pary 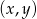(x ,y) wylosowanych kul. Pierwszą kulę możemy wybrać na 5 sposobów, a drugą na 4 sposoby, więc jest

5 ⋅4 = 20

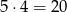
takich par. Są dwa zdarzenia, w których nie ma kuli czerwonej:

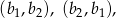
(b1,b2), (b 2,b1),

więc interesujące nas prawdopodobieństwo jest równe

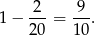
2 9 1 − ---= ---. 20 1 0

Sposób III

Rysujemy drzewko opisujące przebieg losowania

PIC

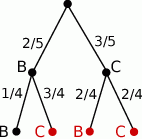
Z drzewka odczytujemy interesujące nas prawdopodobieństwo

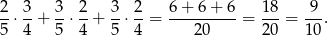
2 3 3 2 3 2 6+ 6+ 6 18 9 -⋅ --+ --⋅--+ --⋅--= ----------= ---= ---. 5 4 5 4 5 4 20 20 1 0

 
Odpowiedź: -9 10

Wersja PDF