/Szkoła średnia/Równania/Wykładnicze/Różne

Zadanie nr 4124158

Oblicz sumę wszystkich pierwiastków równania 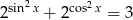sin2x cos2x 2 + 2 = 3 należących do przedziału ⟨0;315⟩ .

Wersja PDF

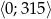Rozwiązanie

Rozwiążmy najpierw podane równanie.

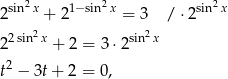
sin2x 1−sin2x sin2x 2 + 2 = 3 / ⋅2 2sin2x sin2x 2 + 2 = 3 ⋅2 t2 − 3t+ 2 = 0,

gdzie 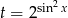t = 2sin2x . Dalej

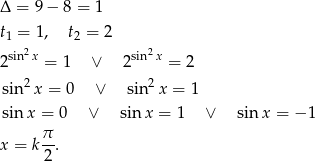
Δ = 9 − 8 = 1 t1 = 1, t2 = 2 2sin2x = 1 ∨ 2sin2x = 2 sin 2x = 0 ∨ sin 2x = 1 sin x = 0 ∨ sin x = 1 ∨ sin x = −1 x = kπ-. 2

Mamy więc ciąg arytmetyczny 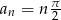π an = n-2 . Ponieważ

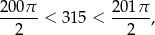
2 00π 201π ------< 315 < -----, 2 2

to musimy obliczyć sumę jego 200 początkowych wyrazów (pierwiastkiem 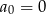a0 = 0 możemy się nie przejmować, bo nie zmienia sumy). Suma ta jest równa

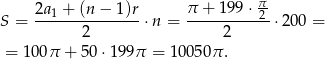
2a + (n − 1)r π + 199 ⋅ π S = ---1-----------⋅n = ----------2-⋅20 0 = 2 2 = 100π + 50 ⋅199π = 1005 0π.

 
Odpowiedź: 100 50π

Wersja PDF