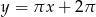/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Wzajemne położenie prostych

Zadanie nr 4377774

Dodaj do ulubionych
Dodaj do rozwiązanych

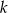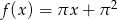Prosta k jest wykresem funkcji 2 f (x) = πx + π .

  • Oblicz współrzędne punktu przecięcia prostej k z wykresem funkcji g(x) = x + π .
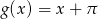  • Znajdź równanie prostej przechodzącej przez punkt 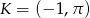K = (− 1,π ) i równoległej do prostej k .

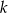Rozwiązanie

  • Musimy rozwiązać układ równań
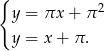
    { y = πx + π 2 y = x + π.

    Odejmując od pierwszego równania drugie (żeby skrócić 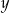y ) mamy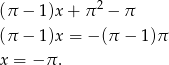

    (π − 1 )x+ π2 − π (π − 1 )x = − (π − 1)π x = − π .

    Z drugiego równania mamy y = x + π = 0 .  
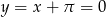    Odpowiedź: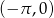 (− π,0)

  • Szukamy prostej w postaci 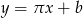y = πx + b . Współczynnik 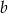b wyznaczymy oczywiście z podanego punktu na tej prostej.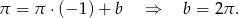
    π = π ⋅(− 1) + b ⇒ b = 2π.

     
    Odpowiedź: y = πx + 2π

Wersja PDF