/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Wzajemne położenie prostych

Zadanie nr 9383116

Dodaj do ulubionych
Dodaj do rozwiązanych

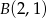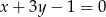Zapisz równanie prostej przechodzącej przez punkt B(2 ,1) i prostopadłej do prostej danej równaniem x + 3y − 1 = 0 .

Rozwiązanie

Będziemy korzystać z faktu, że dwie proste

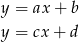
y = ax + b y = cx + d

są prostopadłe wtedy i tylko wtedy gdy 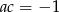ac = − 1 .

Zapiszmy najpierw podane równanie w postaci kierunkowej.

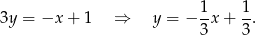
1- 1- 3y = −x + 1 ⇒ y = − 3x + 3 .

Na mocy uwagi na początku, szukamy prostej postaci 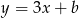y = 3x + b . Współczynnik 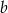b wyznaczamy z informacji o tym, że prosta ta przechodzi przez 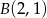B (2,1) (wstawiamy jego współrzędne do równania prostej).

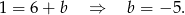
1 = 6+ b ⇒ b = − 5.

 
Odpowiedź: y = 3x− 5

Wersja PDF