/Szkoła średnia/Funkcje/Wielomiany/Stopnia 4/Rozkład

Zadanie nr 2245045

Dodaj do ulubionych
Dodaj do rozwiązanych

Przedstaw wielomian 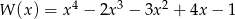4 3 2 W (x) = x − 2x − 3x + 4x − 1 w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.

Rozwiązanie

Po pierwsze warto sprawdzić czy dany wielomian nie ma przypadkiem pierwiastków całkowitych – gdyby miał, to możemy stosować standardowe metody rozkładania wielomianu. Ze względu na wyraz wolny w rachubę wchodzą tylko -1 i 1. Niestety żadna z tych liczb nie jest pierwiastkiem 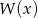W (x ) . Musimy więc poradzić sobie inaczej.

Zapiszemy wielomian jako różnicę dwóch kwadratów i skorzystamy ze wzoru 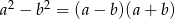a2 − b2 = (a − b)(a + b) . Chwila kombinowania i robimy tak:

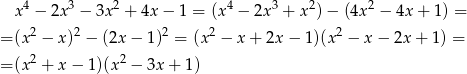
x4 − 2x3 − 3x2 + 4x − 1 = (x4 − 2x3 + x2) − (4x2 − 4x + 1) = 2 2 2 2 2 = (x − x) − (2x − 1) = (x − x + 2x − 1)(x − x− 2x + 1) = = (x2 + x − 1)(x2 − 3x + 1)

 
Odpowiedź: 2 2 (x + x − 1)(x − 3x + 1)

Wersja PDF