/Konkursy/Zadania/Kombinatoryka

Zadanie nr 2604950

Grupa szachistów postanowiła zorganizować turniej szachowy w systemie każdy z każdym. Rozgrywano 5 partii dziennie. Turniej trwał 9 dni. Ilu szachistów brało w nim udział ?

Wersja PDF

Rozwiązanie

Z podanych informacji wynika, że w sumie rozegrano 45 partii.

Sposób I

Z drugiej strony, jeżeli było n szachistów, to wszystkich partii rozegrano

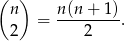
(n ) n (n+ 1) = ---------. 2 2

Mamy zatem równanie

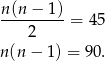
n(n-−-1)-= 45 2 n(n − 1) = 9 0.

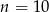Łatwo zgadnąć jego rozwiązanie (bo n ma być całkowite!), n = 10 . Jeżeli ktoś nie umie zgadywać, to oczywiście może rozwiązać z Δ -y.

Sposób II

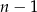Jeżeli szachistów jest n to każdy z nich rozegrał n − 1 partii. W sumie rozegrano więc 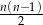n(n−-1) 2 partii (dzielimy przez dwa, bo mnożąc 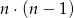n ⋅(n − 1) liczymy każdą partię podwójnie). Dalej rozwiązujemy jak w poprzednim sposobie.  
Odpowiedź: Dziesięciu

Wersja PDF