/Konkursy/Zadania/Kombinatoryka

Zadanie nr 7427189

Dodaj do ulubionych
Dodaj do rozwiązanych

Na ile sposobów można zapłacić 250 zł monetami 1,2 i 5 złotowymi?

Rozwiązanie

Wszystkie możliwe przedstawienia 250zł jako sumy 1,2 i 5 złotówek podzielimy ze względu na ilość 5-złotówek. Na koniec wszystko dodamy. 5-złotówek może być od 0 do 50. Dla każdej z tych wartości zastanowimy się ile może być 2-złotówek. Gdy ustalimy już ilość 2 i 5-złotówek, to ilość 1-złotówek będzie ustalona - nie ma tam już żadnego wyboru. No to liczymy.

Ilość
5-złotówek 		Kwota dla
1,2-złotówek		 Możliwości wyboru
2-złotówek
0 250 126
1 245 123
2 240 121
3 235 118
4 230 116
…
47 15 8
48 10 6
49 5 3
50 0 1

Wystarczy teraz dodać liczby w ostatniej kolumnie. Aby to zrobić zauważmy, że mamy tam dwa ciągi arytmetyczne o różnicy 5:

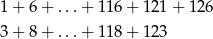
1 + 6 + ...+ 116 + 121 + 126 3 + 8 + ...+ 118 + 123

Ich sumy to odpowiednio:

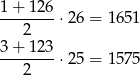
1 + 1 26 -------- ⋅26 = 165 1 2 3-+-1-23 ⋅25 = 157 5 2

Czyli razem 3226.
Uwaga. Całe rozwiązanie można zgrabniej zapisać przy pomocy symbolu sumy 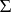Σ . Szukana ilośc jest równa

( [ ] ) 50 2 50− 5x ∑ --------- + 1 x=0 2

gdzie x –liczba pięciozłotówek a [x ] -oznacza część całkowitą liczby x . Wyrażenie w nawiasie to liczba możliwych wyborów 2-złotówek przy ustalonym x . Aby obliczyć tę sumę, trzeba ją rozbić na dwie części, gdy x jest parzysty i nieparzysty. Szczegóły zostawiamy jako ćwiczenie.  
Odpowiedź: 3226

Wersja PDF