Zadanie nr 8789622
Turnieju tenisowego rozgrywanego systemem każdy z każdym nie ukończyło dwóch graczy. Jeden z nich rozegrał tylko jeden mecz, a drugi dziesięć meczy. Ilu zawodników przystąpiło do turnieju, jeżeli wiadomo, że rozegrano 55 meczy? Czy zawodnicy, którzy nie ukończyli turnieju rozegrali ze sobą mecz?
Rozwiązanie
Oznaczmy szukaną liczbę zawodników przez  . Z treści wiemy, że
. Z treści wiemy, że 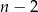 z nich rozegrało mecze każdy z każdym. Ile było tych meczy? Dokładnie
z nich rozegrało mecze każdy z każdym. Ile było tych meczy? Dokładnie
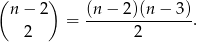
To jednak nie wszystko, bo są jeszcze mecze rozegrane przez dwóch, osobno opisanych zawodników. Ile ich trzeba dołożyć? Na pewno co najmniej 10 meczy rozegranych przez drugiego z tych zawodników. Teraz wszystko zależy od tego czy ci dwaj specjalni zawodnicy rozegrali ze sobą mecz. Jeżeli rozegrali, to ten 1 mecz pierwszego zawodnika już policzyliśmy, a jeżeli nie rozegrali to trzeba go dodać. Żeby dwa razy nie przepisywać tego samego, oznaczmy przez  liczbę 0 lub 1, w zależności od tego czy Ci dwaj zawodnicy rozegrali mecz. Mamy więc równanie
liczbę 0 lub 1, w zależności od tego czy Ci dwaj zawodnicy rozegrali mecz. Mamy więc równanie
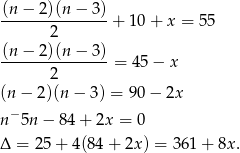
Teraz sprawdzamy, dla 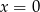 mamy
mamy 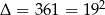 , a dla
, a dla 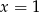 mamy
mamy 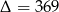 i nie jest to kwadrat liczby całkowitej, co oznacza, że w tym przypadku równanie nie ma rozwiązań całkowitych. Zatem
i nie jest to kwadrat liczby całkowitej, co oznacza, że w tym przypadku równanie nie ma rozwiązań całkowitych. Zatem 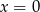 i mamy
i mamy
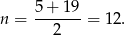
Odpowiedź: Dwunastu. Tak, rozegrali.

