Zadanie nr 9765802
Uzasadnić, że  prostych może podzielić płaszczyznę na maksymalnie
prostych może podzielić płaszczyznę na maksymalnie 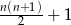 obszarów.
obszarów.
Rozwiązanie
Sposób I
Jeżeli oznaczymy maksymalną liczbę obszarów, na które może podzielić płaszczyznę  prostych, to mamy
prostych, to mamy 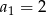 oraz
oraz 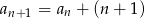 . Spróbujmy wyjaśnić tę drugą równość. Prowadząc
. Spróbujmy wyjaśnić tę drugą równość. Prowadząc 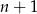 prostą, przetniemy co najwyżej
prostą, przetniemy co najwyżej  wcześniej narysowanych prostych, czyli
wcześniej narysowanych prostych, czyli 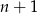 poprzednio istniejących obszarów.
poprzednio istniejących obszarów.
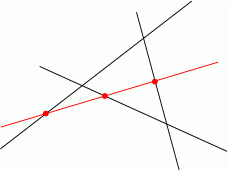
Każdy z tych obszarów dzielimy na dwa, więc dochodzi 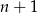 nowych obszarów. Zatem
nowych obszarów. Zatem
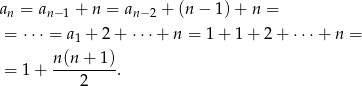
Sposób II
Powyższe rozwiązanie mogliśmy zgrabnie zapisać przy pomocy indukcji.
Dla 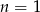 mamy jedną prostą, która dzieli płaszczyznę na 2 obszary. Z drugiej strony
mamy jedną prostą, która dzieli płaszczyznę na 2 obszary. Z drugiej strony
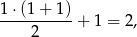
czyli się zgadza.
Załóżmy teraz, że  prostych dzieli płaszczyznę na co najwyżej
prostych dzieli płaszczyznę na co najwyżej 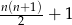 obszarów. Podobnie jak w poprzednim sposobie zauważamy, że prowadząc
obszarów. Podobnie jak w poprzednim sposobie zauważamy, że prowadząc 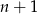 prostą tworzymy co najwyżej
prostą tworzymy co najwyżej 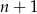 nowych obszarów (bo prosta ta przecina co najwyżej
nowych obszarów (bo prosta ta przecina co najwyżej  prostych, czyli
prostych, czyli 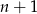 obszarów). Zatem
obszarów). Zatem 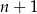 prostych dzieli płaszczyznę na co najwyżej
prostych dzieli płaszczyznę na co najwyżej
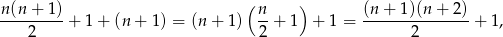
co kończy dowód indukcyjny.

