/Szkoła średnia/Funkcje - wykresy/Homografia

Zadanie nr 1277909

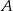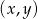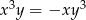  • Zaznacz w układzie współrzędnych zbiór A punktów, których współrzędne (x ,y) spełniają warunek: x3y = −xy 3 .
  • Wiedząc, że wykres funkcji homograficznej 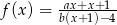f(x ) = -ax+x-+1- b(x+ 1)−4 nie ma punktów wspólnych ze zbiorem 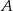A wyznacz a i b .
PIC
Wersja PDF

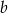Rozwiązanie

  • Podaną równość możemy zapisać w postaci
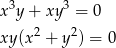
    3 3 x y+ xy = 0 xy(x2 + y2) = 0

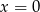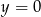    co oznacza, że x = 0 lub y = 0 . Zatem zbiór 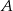A składa się z osi układu współrzędnych.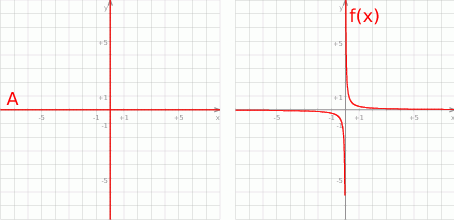

    PIC
  • Z podanej informacji wiemy, że 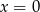x = 0 nie należy do dziedziny funkcji 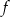f , zatem musi to być miejsce zerowe mianownika. Stąd
    b − 4 = 0 ⇒ b = 4

    i funkcja ma postać

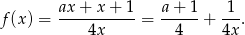
    ax + x + 1 a+ 1 1 f(x) = -----------= -----+ ---. 4x 4 4x

    Wykresem funkcji 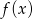f (x) jest więc hiperbola 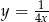1 y = 4x przesunięta o 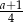a+ 1 -4-- wzdłuż osi 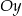Oy . Skoro wiemy, że 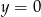y = 0 nie jest wartością funkcji, więc musi być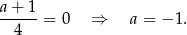

    a+ 1 ------= 0 ⇒ a = − 1. 4

     
    Odpowiedź: a = − 1, b = 4

Wersja PDF