Zadanie nr 2000586
Na rysunku obok przedstawiony jest fragment wykresu funkcji 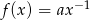 , gdzie
, gdzie 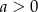 . Rozpatrzmy figury
. Rozpatrzmy figury 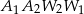 i
i 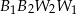 , gdzie
, gdzie 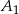 i
i 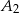 są dowolnymi różnymi punktami na dodatniej półosi osi
są dowolnymi różnymi punktami na dodatniej półosi osi 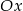 . Udowodnij, że figury te mają równe pola.
. Udowodnij, że figury te mają równe pola.
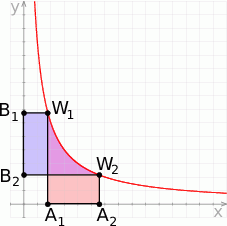
Rozwiązanie
Z rysunku widać, że wystarczy wykazać, że pola zacieniowanych prostokątów są równe. Jeżeli 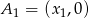 i
i 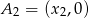 , to
, to 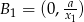 i
i 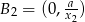 i pola tych prostokątów są odpowiednio równe
i pola tych prostokątów są odpowiednio równe
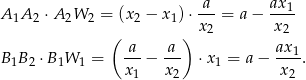
Widać, że pola te są równe.

