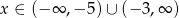Zadanie nr 2875082
Wykres funkcji 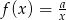 dla
dla 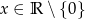 , gdzie
, gdzie 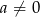 , przesunięto o wektor
, przesunięto o wektor ![→u = [− 3,2]](https://img.zadania.info/zad/2875082/HzadT3x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 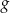 . Do wykresu funkcji
. Do wykresu funkcji 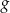 należy punkt
należy punkt 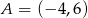 . Oblicz
. Oblicz  , następnie rozwiąż nierówność
, następnie rozwiąż nierówność 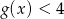 .
.
Rozwiązanie
Korzystamy ze wzoru na przesunięcie funkcji 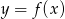 o wektor
o wektor ![→ v = [a,b]](https://img.zadania.info/zad/2875082/HzadR1x.gif) :
:
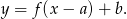
Z powyższego wzoru 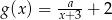 . Informacja o punkcie
. Informacja o punkcie 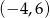 na wykresie tej funkcji daje nam równanie
na wykresie tej funkcji daje nam równanie
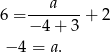
Pozostało rozwiązać nierówność
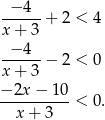
Ostatnia nierówność jest równoważna nierówności
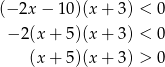
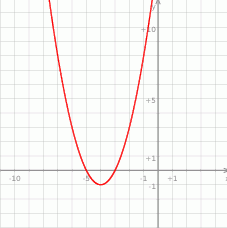
a to jest już zwykła parabola (rysunek) czyli 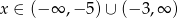 .
.
Odpowiedź: 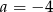 ,
,