Zadanie nr 5074509
Wykres funkcji 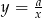 , gdzie
, gdzie 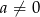 przesunięto o wektor
przesunięto o wektor ![[2,3]](https://img.zadania.info/zad/5074509/HzadT2x.gif) i otrzymano wykres funkcji, która ma dokładnie dwa punkty wspólne z okręgiem o równaniu
i otrzymano wykres funkcji, która ma dokładnie dwa punkty wspólne z okręgiem o równaniu 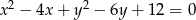 . Wyznacz
. Wyznacz  .
.
Rozwiązanie
Przesuwając wykres funkcji 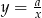 o wektor
o wektor ![[2,3]](https://img.zadania.info/zad/5074509/HzadR1x.gif) otrzymamy wykres funkcji
otrzymamy wykres funkcji
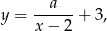
czyli hiperbolę o asymptotach 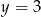 i
i 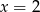 . Aby naszkicować podany okrąg, przekształćmy jego równanie
. Aby naszkicować podany okrąg, przekształćmy jego równanie
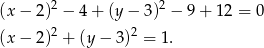
Jest to więc okrąg o promieniu 1 i środku w punkcie 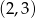 . Teraz możemy naszkicować opisaną sytuację.
. Teraz możemy naszkicować opisaną sytuację.
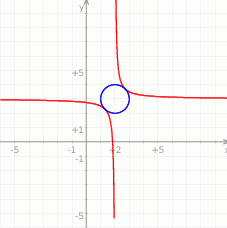
Punkty wspólne tych dwóch krzywych znajdujemy podstawiając 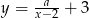 do równania okręgu.
do równania okręgu.
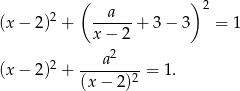
Podstawmy teraz 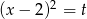 .
.
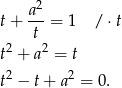
Teraz chwilę się zastanówmy co dalej. Jeżeli powyższe równanie nie ma rozwiązań, lub rozwiązania są ujemne, to interesujące nas krzywe w ogóle się nie przecinają. Jeżeli natomiast równanie ma dwa rozwiązania i przynajmniej jedno jest dodatnie, na mocy wzorów Viète’a ich iloczyn jest równy 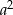 , więc oba są dodatnie (tu jest ważne, że
, więc oba są dodatnie (tu jest ważne, że 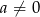 ). To pozwoli jednak wyliczyć 4 wartości
). To pozwoli jednak wyliczyć 4 wartości  , co jest sprzeczne z informacją, że wykresy przecinają się dokładnie w dwóch punktach. Zatem powyższe równanie musi mieć dokładnie jeden pierwiastek, czyli musi być
, co jest sprzeczne z informacją, że wykresy przecinają się dokładnie w dwóch punktach. Zatem powyższe równanie musi mieć dokładnie jeden pierwiastek, czyli musi być 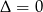 .
.
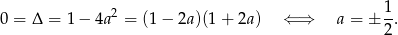
Odpowiedź: 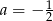 lub
lub