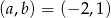/Szkoła średnia/Funkcje - wykresy/Homografia

Zadanie nr 9993947

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykres funkcji homograficznej 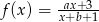-ax+3- f(x ) = x+b+ 1 można otrzymać przesuwając wykres funkcji 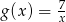g(x) = 7x , a dziedzina funkcji 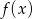f(x) jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki a i b .

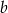Rozwiązanie

Zapiszmy wzór funkcji 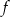f w postaci kanonicznej.

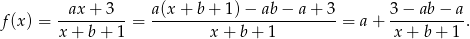
ax + 3 a(x+ b+ 1)− ab− a+ 3 3 − ab − a f(x) = ----------= -------------------------= a + ----------. x + b+ 1 x+ b+ 1 x+ b+ 1

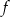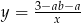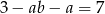Widać teraz, że wykres funkcji f powstaje z wykresu funkcji y = 3−abx−a- przez przesunięcie o wektor [−b − 1,a] . To daje nam równanie 3− ab− a = 7 .

Z postaci kanonicznej widać także, że dziedziną funkcji 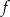f jest zbiór 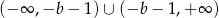(− ∞ ,−b − 1)∪ (−b − 1 ,+ ∞ ) , a jej zbiorem wartości zbiór 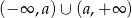(− ∞ ,a)∪ (a,+ ∞ ) . Wiemy, że dziedzina ma być tym samym zbiorem co zbiór wartości, czyli 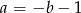a = −b − 1 . Mamy zatem układ równań

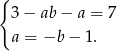
{ 3− ab− a = 7 a = −b − 1.

Podstawiamy 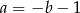a = −b − 1 z drugiego równania do pierwszego.

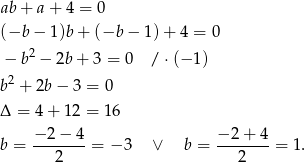
ab + a + 4 = 0 (−b − 1)b + (−b − 1)+ 4 = 0 2 − b − 2b+ 3 = 0 /⋅ (− 1) b2 + 2b − 3 = 0 Δ = 4+ 12 = 16 − 2− 4 − 2+ 4 b = -------= − 3 ∨ b = ------- = 1. 2 2

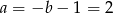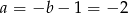Mamy wtedy odpowiednio a = −b − 1 = 2 i a = −b − 1 = − 2 . Na koniec obrazek dla ciekawskich.

PIC

 
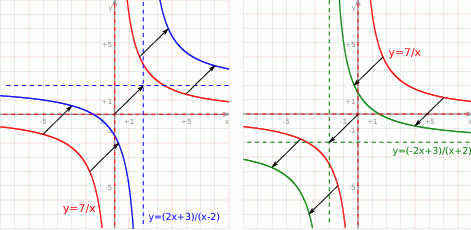
Odpowiedź: 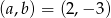(a,b) = (2 ,− 3 ) lub (a,b) = (− 2,1)

Wersja PDF