Zadanie nr 1059166

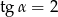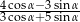Wiedząc, że jest kątem ostrym i tgα = 2 , oblicz wartość wyrażenia 43-cocossαα−+-35ssininαα .

Rozwiązanie

Sposób I

Ponieważ mamy podany tangens, podzielmy licznik i mianownik danego ułamka przez 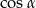cosα .

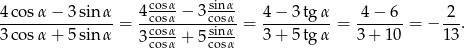
4 cosα − 3sinα 4 cocossαα-− 3 scoinsαα- 4 − 3 tg α 4− 6 2 ---------------- = --cosα-----sinα-= ----------= -------= − --. 3 cosα + 5sinα 3 cosα + 5 cosα 3 + 5 tg α 3 + 10 13

Sposób II

Zauważmy, że

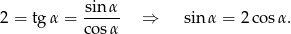
sin α 2 = tg α = co-sα ⇒ sinα = 2co sα.

Zatem

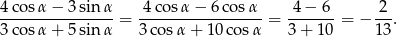
4-cosα-−-3-sin-α- -4cos-α−--6co-sα- -4−--6- -2- 3 cosα + 5 sin α = 3co sα + 10 cosα = 3 + 10 = − 13 .

Sposób III

Jeżeli zabrakło nam sprytu potrzebnego do poprzednich sposobów, możemy z podanego tangensa wyliczyć 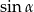sin α i cosα .

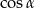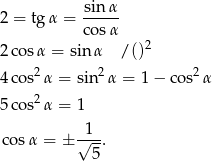
sinα- 2 = tgα = cosα 2 2 cos α = sinα /() 4 cos2 α = sin2α = 1− cos2α 2 5 cos α = 1 1 cosα = ± √--. 5

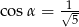Ponieważ jest kątem ostrym, -1- cosα = √ 5 . Stąd (ponownie korzystamy z tego, że jest kątem ostrym)

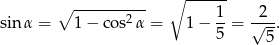
∘ ------ ∘ -------2-- 1- -2-- sin α = 1 − cos α = 1 − 5 = √ --. 5

Możemy teraz obliczyć wartość podanego wyrażenia

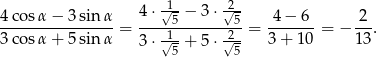
4 ⋅√1-− 3⋅ 2√-- 4-cosα-−--3sinα- = -----5-------5 = -4−-6--= − 2-. 3 cosα + 5sinα 3 ⋅√1-+ 5⋅ 2√-- 3 + 10 13 5 5

Odpowiedź: -2 − 13