Zadanie nr 1112764
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to
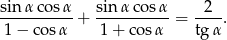
Rozwiązanie
Przekształcamy lewą stronę danej równości tak, aby dojść do prawej strony.
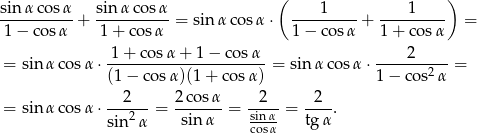
Po drodze skorzystaliśmy z jedynki trygonometrycznej 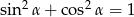 i równości
i równości 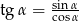 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to
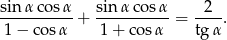
Przekształcamy lewą stronę danej równości tak, aby dojść do prawej strony.
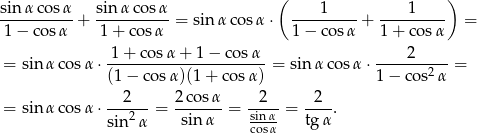
Po drodze skorzystaliśmy z jedynki trygonometrycznej 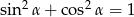 i równości
i równości 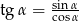 .
.
