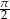/Szkoła średnia/Funkcje/Trygonometryczna

Zadanie nr 2013335

Wyznacz okres podstawowy funkcji 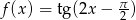π- f (x) = tg(2x − 2) .

Wersja PDF

Rozwiązanie

Sposób I

Okresem podstawowym funkcji 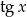tg x jest liczba 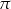π . Szukamy zatem takiego 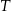T , że

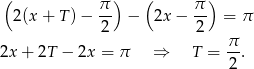
( π ) ( π ) 2 (x+ T) − -- − 2x − -- = π 2 2 2x+ 2T − 2x = π ⇒ T = π-. 2

Sposób II

Ponieważ

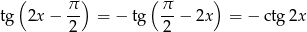
( ) ( ) tg 2x − π- = − tg π-− 2x = − ctg2x 2 2

to widać, że okres jest dwa razy krótszy niż okres 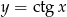y = ctg x . Okres jest więc równy π- 2 .  
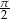Odpowiedź: π- 2

Wersja PDF