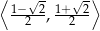Zadanie nr 2454938
Wyznacz zbiór wartości funkcji 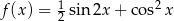 , gdzie
, gdzie 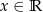 .
.
Rozwiązanie
Skorzystamy najpierw ze wzoru na cosinus podwojonego kąta
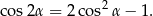
To pozwala nam przekształcić wzór funkcji 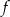 tak, aby obie funkcje trygonometryczne miały ten sam argument.
tak, aby obie funkcje trygonometryczne miały ten sam argument.
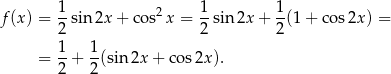
Dalszą część rozwiązania przeprowadzimy na dwa sposoby.
Sposób I
Będziemy przekształcać wzór funkcji 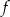 tak, aby móc skorzystać ze wzoru na sumę sinusów.
tak, aby móc skorzystać ze wzoru na sumę sinusów.
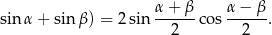
Przekształcamy
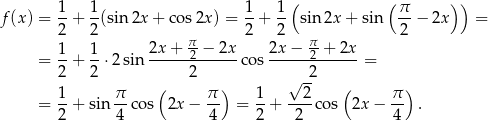
Ponieważ zbiorem wartości wyrażenia 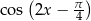 jest przedział
jest przedział 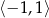 , to zbiorem wartości funkcji
, to zbiorem wartości funkcji 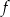 jest przedział
jest przedział
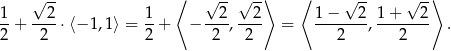
Sposób II
Tym razem skorzystamy ze wzoru na sinus sumy
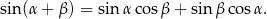
Mamy zatem
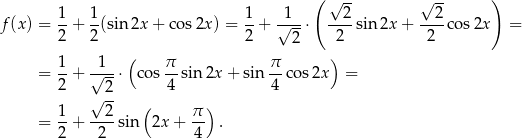
Podobnie jak w poprzednim sposobie, wnioskujemy stąd, że zbiorem wartości funkcji 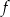 jest
jest
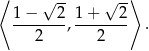
Odpowiedź: