/Szkoła średnia/Funkcje/Trygonometryczna

Zadanie nr 2566953

Dodaj do ulubionych
Dodaj do rozwiązanych

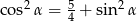Wykaż, że nie istnieje kąt ostry α taki, że 2 5 2 cos α = 4 + sin α .

Rozwiązanie

Sposób I

Korzystamy z jedynki trygonometrycznej.

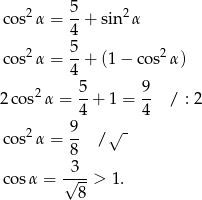
5 cos2α = --+ sin2α 4 cos2α = 5-+ (1 − cos2α ) 4 2 5 9 2 cos α = --+ 1 = -- / : 2 4 4 cos2α = 9- / √ - 8 -3-- cosα = √ 8-> 1 .

To jednak jest sprzeczność, bo zawsze 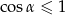co sα ≤ 1 .

Sposób II

Korzystamy z jedynki trygonometrycznej.

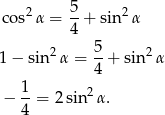
2 5- 2 cos α = 4 + sin α 5 1− sin 2α = -+ sin 2α 4 − 1-= 2 sin 2α. 4

To oczywiście nie jest możliwe, bo kwadrat liczby jest zawsze nieujemny.

Sposób III

Korzystamy ze wzoru na 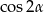cos 2α .

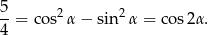
5 2 2 --= co s α − sin α = cos2α . 4

To jednak jest niemożliwe, bo 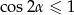cos2α ≤ 1 .

Sposób IV

Narysujmy trójkąt prostokątny.

PIC

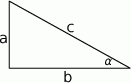
Liczymy (korzystamy z twierdzenia Pitagorasa)

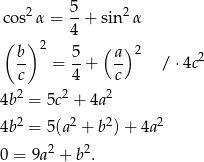
5 co s2α = -+ sin 2α ( )2 4 b- 5- ( a)2 2 c = 4 + c / ⋅4c 2 2 2 4b = 5c + 4a 4b2 = 5(a 2 + b2) + 4a2 0 = 9a2 + b2.

Prawa strona jest liczbą dodatnią, więc powyższa równość nie może być spełniona.

Wersja PDF