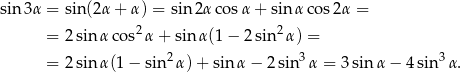Zadanie nr 2918068
Wykaż, że 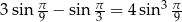 .
.
Rozwiązanie
Korzystamy ze wzorów
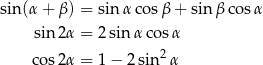
Sposób I
Korzystamy z powyższych wzorów
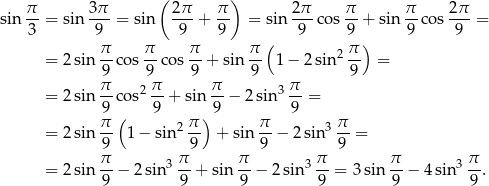
Zatem rzeczywiście
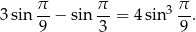
Sposób II
Jeżeli powyższy rachunek wygląda na trochę przytłaczający, to możemy jego zapis trochę uprościć. Jeżeli oznaczymy 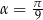 , to musimy wykazać, że
, to musimy wykazać, że
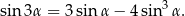
Przekształcamy lewą stronę tak samo jak w pierwszym sposobie.