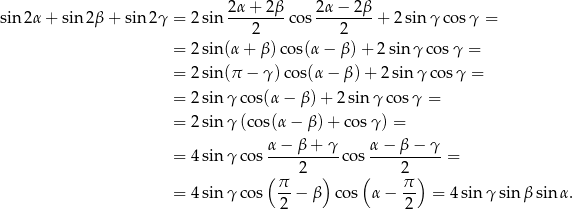Zadanie nr 3124410

Udowodnij, że jeżeli 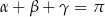α+ β+ γ = π , to

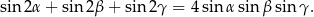
sin 2α + sin2β + sin 2γ = 4sin αsinβ sin γ.

Wersja PDF

Rozwiązanie

Korzystamy ze wzorów

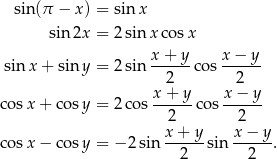
sin (π − x) = sin x sin 2x = 2sinx cos x x+ y x − y sin x+ sin y = 2sin ------cos------ 2 2 cosx + cosy = 2cos x-+-y-cos x−--y- 2 2 x+--y- x-−-y- cosx − cosy = −2 sin 2 sin 2 .

Sposób I

Przekształcamy równość, którą mamy udowodnić, w sposób równoważny – podstawiamy 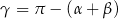γ = π − (α+ β)

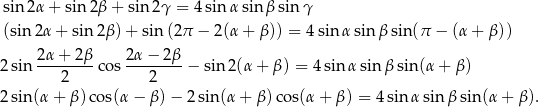
sin 2α+ sin 2β + sin 2γ = 4sinα sinβ sin γ (sin 2α+ sin 2β )+ sin (2π − 2(α + β)) = 4 sin α sin β sin (π − (α + β)) 2sin 2α-+-2β-co s 2α-−-2β-− sin 2(α + β ) = 4sin αsin βsin(α + β ) 2 2 2sin(α + β )cos(α − β )− 2sin(α + β) cos(α + β) = 4sinα sinβ sin(α + β )&#

Po obu tronach tej równości mamy wspólny czynnik 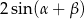2sin(α + β ) , więc pozostało udowodnić, że

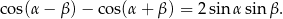
co s(α− β) − cos(α + β ) = 2sin αsin β.

Ta równość wynika natychmiast ze wzoru na różnicę cosinusów:

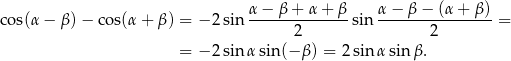
α-−-β-+-α-+-β- α−--β-−-(α-+-β)- cos(α − β) − cos(α + β ) = − 2sin 2 sin 2 = = − 2sin αsin(− β ) = 2sin αsin β.

Sposób II

Próbujemy przekształcić lewą stronę tak, aby zamienić znajdujące się tam wyrażenie na postać iloczynową.

sin 2α + sin 2β + sin2γ = 2 sin 2α-+-2-β cos 2-α−-2β + 2 sin γ cosγ = 2 2 = 2 sin (α+ β)co s(α− β)+ 2sin γco sγ = = 2 sin (π − γ )cos(α − β )+ 2 sin γ cos γ = = 2 sin γ cos(α − β) + 2 sin γ cos γ = = 2 sin γ (cos(α − β) + cos γ) = α− β + γ α − β − γ = 4 sin γ cos ----------cos ----------= ( π 2 ) ( 2π ) = 4 sin γ cos --− β cos α − -- = 4sin γsin β sin α. 2 2