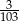Zadanie nr 4271297
Kąt  jest ostry i
jest ostry i 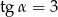 . Oblicz
. Oblicz 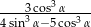 .
.
Rozwiązanie
Sposób I
Ponieważ mamy podany tangens, podzielmy licznik i mianownik danego ułamka przez 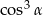 .
.
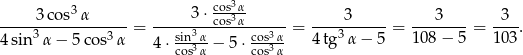
Sposób II
Zauważmy, że
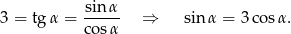
Zatem
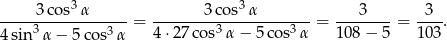
Odpowiedź: 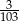
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Kąt  jest ostry i
jest ostry i 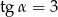 . Oblicz
. Oblicz 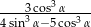 .
.
Sposób I
Ponieważ mamy podany tangens, podzielmy licznik i mianownik danego ułamka przez 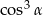 .
.
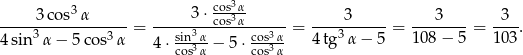
Sposób II
Zauważmy, że
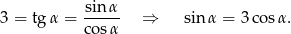
Zatem
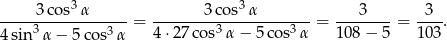
Odpowiedź: